總曲率是數學和物理學中一個比較重要的概念。
基本介紹
- 中文名:總曲率
- 分類:數理科學
簡介
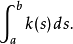
總曲率是數學和物理學中一個比較重要的概念。
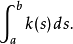
總曲率是數學和物理學中一個比較重要的概念。...... 在數學中的曲線微分幾何的研究中, 一個浸入在平面上的曲線的總曲率是曲率的曲線積分:閉曲線的總曲率是 2π...
曲線的曲率(curvature)就是針對曲線上某個點的切線方向角對弧長的轉動率,通過微分來定義,表明曲線偏離直線的程度。數學上表明曲線在某一點的彎曲程度的數值。曲率越...
過曲面上某個點上具有無窮個正交曲率,其中存在一條曲線使得該曲線的曲率為極大,這個曲率為極大值Kmax ,垂直於極大曲率面的曲率為極小值Kmin。這兩個曲率屬性...
微分幾何中,曲面上一點的高斯曲率是該點主曲率κ1和κ2的乘積。它是曲率的內在度量,也即,它的值只依賴於曲面上的距離如何測量,而不是曲面如何嵌入到空間。這個...
常曲率曲面有常高斯曲率曲面和常平均曲率曲面。一般常曲率曲面指的是常高斯曲率曲面。一個高斯曲率在各點上均取相同值的曲面,我們稱這曲面為常高斯曲率的曲面。...
空間曲率可以這樣定義:廣義相對論里,光是沿任意兩點間的最短距離傳播的,所以光線的彎曲的曲率就代表了空間彎曲的曲率。當然空間被彎曲意味著無數的平面被彎曲,定義...
氣旋性曲率是在氣象上流體呈反時針方向(在北半球)移動的軌跡的曲率,並規定為正值;反之,呈順時針方向旋轉時的曲率為負,並稱為反氣旋式曲率。在南半球則定義相反...
李普希茨一基靈曲率(Lipschitz-Killing curva-ture) R3中曲面的總曲率的推廣.歐氏空間中子流形關於一個單位法向量場的所有主曲率之積.設M"是R,.+-n中的n維...
5 撓率和曲率的區別 撓率簡介 編輯 撓率,它的絕對值度量了曲線上鄰近兩點的次法向量之間的夾角對弧長的變化率。平面曲線是撓率恆為零的曲線。空間曲線如不是落在...
高斯絕妙定理(Gauss theorem egregium),表達高斯曲率的一個定理。曲面的高斯曲率K可以用曲面的第一類基本量及它們的一階、二階偏導數來表示,因此,高斯曲率是曲面的...
若曲面上的一點P,其第一、二基本形式成比例,則稱P點為曲面的臍點(umbilical point)。若第二基本形式為零,則稱為平點,否則稱為圓點。在臍點處總曲率K=H2(...
關於正則閉曲線的全曲率的界限有下述二定理。富勒氏曲線芬切爾定理 正則閉曲線C的全曲率≥2,且等號僅當C為平面凸閉曲線時成立。這定理給出了正則閉曲線的全曲率的...
