基本介紹
- 中文名:高斯曲率
- 外文名:Gauss curvature
- 意義:反映曲面的彎曲程度
- 領域:數理科學
- 相關定理:高斯絕妙定理;高斯-博內定理
定義





 圖1.高斯曲率曲面
圖1.高斯曲率曲面非形式化定義
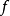

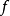

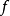

總曲率
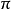

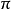
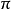

 圖2.負曲率曲面
圖2.負曲率曲面重要定理
1.絕妙定理






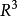

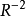
2.高斯-博內定理
常曲率曲面
其它公式






曲面造型上的套用
 圖3.典型的高斯曲率分析結果
圖3.典型的高斯曲率分析結果





 圖1.高斯曲率曲面
圖1.高斯曲率曲面

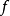

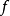

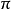

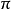
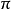

 圖2.負曲率曲面
圖2.負曲率曲面





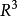

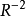






 圖3.典型的高斯曲率分析結果
圖3.典型的高斯曲率分析結果微分幾何中,曲面上一點的高斯曲率是該點主曲率κ1和κ2的乘積。它是曲率的內在度量,也即,它的值只依賴於曲面上的距離如何測量,而不是曲面如何嵌入到空間。這個...
常曲率曲面有常高斯曲率曲面和常平均曲率曲面。一般常曲率曲面指的是常高斯曲率曲面。一個高斯曲率在各點上均取相同值的曲面,我們稱這曲面為常高斯曲率的曲面。...
過曲面上某個點上具有無窮個正交曲率,其中存在一條曲線使得該曲線的曲率為極大,這個曲率為極大值Kmax ,垂直於極大曲率面的曲率為極小值Kmin。這兩個曲率屬性...
空間曲率指某種給定度規的空間對於歐氏空間的偏離程度的量。...... 在這兩個方向上曲率1/R,分別達到極大值和極小值1/R1和1/R2。量稱為高斯曲率。 曲率 ...
高斯曲線,又叫做gaussian curve,是常態分配中的一條標準曲線。...... 一般的葉面是扁平的,而沒有缺口或摺疊,說明了近似零的高斯曲率,平面的勻質生長,例如相同膨脹...
在黎曼幾何中,復曲率(或Ricci標量)是黎曼流形的最簡單的曲率不變數。 對於黎曼流形的每個點,它分配由該點附近的歧管的固有幾何確定的單個實數。 具體來說,復...
二次曲率,,曲率的倒數就是曲率半徑。...... 而對於圓,曲率不隨位置變化。二次曲率詳細信息 編輯 微分幾何中,曲面上一點的高斯曲率是該點主曲率κ1和κ2的乘積...
曲率是刻畫流形的重要幾何量。里奇曲率(Ricci curvature)是n維黎曼流形的n-1個截面曲率的和。...
高斯方程是子流形的基本方程。第一基本型和第二基本型構成曲面的完全不變數系統。即: 如果兩張曲面有相同的第一基本型和第二基本型,則它們在三維歐幾里得空間的...
高斯—波涅公式(Gauss–Bonnet formula)也叫高斯—波涅定理(Gauss–Bonnet theorem),是微分幾何中的重要定理,它描述了內角和與高斯曲率間的關係。公式如下: 推廣 ...
在微分幾何中,高斯-博內定理(亦稱高斯-博內公式)是關於曲面的圖形(由曲率表征)和拓撲(由歐拉示性數表征)間聯繫的一項重要表述。它是以卡爾·弗里德里希·高斯和...
可展曲面是在其上每一點處高斯曲率為零的曲面。微分幾何中的一種特殊曲面。該曲面可以保長變換到平面中去。...
單葉雙曲面的高斯曲率為負,兩片雙曲面的高斯曲率為正。 儘管它具有正曲率,但是具有另一適當選擇的度量的兩張雙曲面也可以用作雙曲線幾何的模型。...
