基本介紹
- 中文名:曲率
- 外文名:curvature
- 全稱:曲線的曲率
- 解釋:曲線某點切線方向對弧長的轉動率
- 曲率表明:曲線偏離直線的程度
- 性質:曲率越大,曲線的彎曲程度越大
- 曲率倒數:曲率半徑
定義
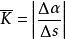



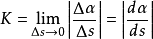

計算公式
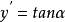


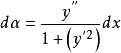
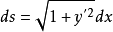

曲率圓與曲率半徑

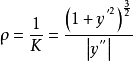



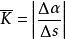



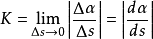

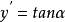


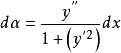
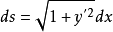


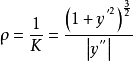


曲線的曲率(curvature)就是針對曲線上某個點的切線方向角對弧長的轉動率,通過微分來定義,表明曲線偏離直線的程度。數學上表明曲線在某一點的彎曲程度的數值。曲率越...
在微分幾何中,曲率的倒數就是曲率半徑,即R=1/K。平面曲線的曲率就是針對曲線上某個點的切線方向角對弧長的轉動率,通過微分來定義,表明曲線偏離直線的程度。對於...
1994年,墨西哥物理學家明戈·阿爾庫貝利(Miguel Alcubierre)首次提出了現實生活中曲率驅動的概念。他所設計的曲率驅動概念包括一個足球形狀的飛船,其周圍是一圈大型的...
過曲面上某個點上具有無窮個正交曲率,其中存在一條曲線使得該曲線的曲率為極大,這個曲率為極大值Kmax ,垂直於極大曲率面的曲率為極小值Kmin。這兩個曲率屬性...
法曲率是刻畫曲面在某一方向的彎曲程度的量,其有一定的計算公式。曲線 C 的曲率和曲面 S 沿 C 的切方向的法曲率具有聯繫。...
空間曲率:表征某種給定度規的空間對於歐氏空間的偏離程度的量。舉例說,球面是一種二維的彎曲空間,球面上弧元的平方是: 。 式中U、嗞 為球面上的點在過球心的...
曲率是刻畫流形的重要幾何量。里奇曲率(Ricci curvature)是n維黎曼流形的n-1個截面曲率的和。...
微分幾何中,曲面上一點的高斯曲率是該點主曲率κ1和κ2的乘積。它是曲率的內在度量,也即,它的值只依賴於曲面上的距離如何測量,而不是曲面如何嵌入到空間。這個...
曲率張量(curvature tensor)由聯絡確定的一個重要張量。曲率張量是一個重要的數學量。在眾人所關注的廣義相對論中起到了重要的作用。沒有曲率張量,就不可能建立起...
所謂曲率驅動的概念就是指通過對時空本身的改造來驅動飛船,利用物理學定律中的漏洞來打破光速不可超越的限制。...
曲率分析的概念 相交的地方線段是不連續的 。...... G3:連續的曲率變換連續(我估計意思是曲率的單次微分連續) G4:連續的曲率變換的連續變換連續(曲率的二次微...
時空曲率是一種科學理論。按照廣義相對論的解釋,在引力場中,時空的性質是由物體的“質量”分布決定的,物體“質量”的分布狀況使時空性質變得不均勻,引起了時空的...
4、不同角膜曲率計的影像設計不同,有的是紅色方格與綠色台階(Javal散光計);有的是兩個軸向垂直的帶十字的圓圈(Bausch-lomb角膜曲率計);有的是空心“十”字與...
在微分幾何中,黎曼曲率張量或黎曼張量是表達黎曼流形的曲率的標準方式,更普遍的,它可以表示有仿射聯絡的流形的曲率 ,包括無扭率或有撓率的。...
地球曲率就是曲線的彎曲程度,如果在曲面上,可以指定某個方向的曲率。曲率愈大,某點在某一方向上的曲率越大。這個用地球做參照物便是指地球半徑的倒數,即1/ ...
平均曲率(mean curvature) 是微分幾何中一個“外在的”彎曲測量標準,局部地描述了一個曲面嵌入周圍空間(比如二維曲面嵌入三維歐幾里得空間)的曲率。平均曲率是空間上...
空間曲率可以這樣定義:廣義相對論里,光是沿任意兩點間的最短距離傳播的,所以光線的彎曲的曲率就代表了空間彎曲的曲率。當然空間被彎曲意味著無數的平面被彎曲,定義...
曲率圖(curvature graph) 是指橫坐標為曲線長,縱坐標為曲率所繪的坐標圖。...... 曲率圖(curvature graph) 是指橫坐標為曲線長,縱坐標為曲率所繪的坐標圖。...
《曲率飛行》是李微胖演唱的一首歌曲...... 《曲率飛行》是李微胖演唱的一首歌曲 中文名稱 曲率飛行 [1] 歌曲原唱 李微胖 [1] 目錄 1 歌曲信息 2 歌曲歌...
在點處的曲線的法線上,在凹的一側取一點 ,使以O為圓心,R為半徑作圓,這個圓包含這一點及其相鄰的那一小段圓弧,這個圓叫做曲線在點處的曲率圓,曲率圓的圓心...
“曲率場”是天文學專有名詞。來自中國天文學名詞審定委員會審定發布的天文學專有名詞中文譯名,詞條譯名和中英文解釋數據著作權由天文學名詞委所有。...
航道曲率,或稱航道彎度曲率,是指航道上彎曲部分的航道中線的圓弧曲率。航道曲率的倒數就是航道曲率半徑。航道彎曲半徑說明航道的彎曲程度。 如彎曲半徑過小,則影響...
在曲線上一點M的的法線上,在凹的一側取一點D ,使DM等於該點處的曲率半徑,以D為圓心,DM為半徑作圓,這個圓叫做曲線在點處的曲率圓。在點M附近,曲率圓弧與...
