曲率圓,又稱密切圓。在曲線上一點M的的法線上,在凹的一側取一點D ,使DM等於該點處的曲率半徑,以D為圓心,DM為半徑作圓,這個圓叫做曲線在點處的曲率圓。在點M附近,曲率圓弧與曲線弧密切程度非常好,所以曲率圓又叫密切圓。
基本介紹
- 中文名:曲率圓
- 外文名:curvature circle
- 別稱:密切圓
- 套用領域:解析幾何
- 位置和大小:曲率中心與曲率半徑
- 作用:切點附近用圓弧代替曲線弧
定義,性質,位置和大小,曲率中心,曲率半徑,
定義
曲率圓與曲線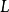 在
在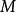 點有相同的切線和凹向以及相同的曲率,因而在
點有相同的切線和凹向以及相同的曲率,因而在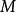 點附近,曲率圓弧與曲線弧密切程度非常好,所以曲率圓又叫密切圓。在實際問題中,常常用曲率圓在點
點附近,曲率圓弧與曲線弧密切程度非常好,所以曲率圓又叫密切圓。在實際問題中,常常用曲率圓在點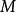 鄰近的一段圓弧來近似地代替曲線弧,使問題簡化。
鄰近的一段圓弧來近似地代替曲線弧,使問題簡化。
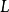
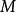
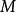
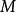
性質
①曲率圓過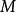 點,且在
點,且在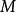 點與曲線相切,即曲率圓與曲線在
點與曲線相切,即曲率圓與曲線在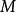 點有相同的切線。
點有相同的切線。
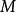
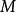
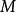
②在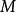 點附近與曲線有相同的凹向。
點附近與曲線有相同的凹向。
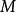
③曲率圓的曲率與曲線在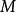 點的曲率相等。
點的曲率相等。
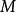
位置和大小
曲率中心
曲率中心確定曲率圓的位置。
設函式 在點
在點 處二階可導,且
處二階可導,且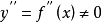 ,曲線
,曲線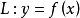 在點
在點 處的曲率中心為
處的曲率中心為 ,則:
,則:


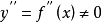
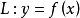



其中,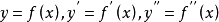 。
。
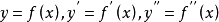
曲率半徑