曲率是刻畫流形的重要幾何量。里奇曲率(Ricci curvature)是n維黎曼流形的n-1個截面曲率的和。
基本介紹
- 中文名:里奇曲率
- 外文名:Ricci curvature
- 適用範圍:數理科學
簡介
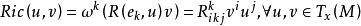
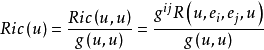

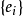
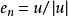
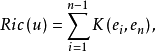
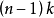
相關概念
數量曲率

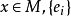

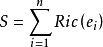

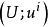
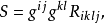
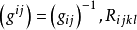
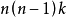
截面曲率

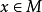
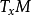
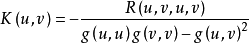
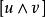
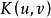
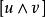

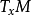
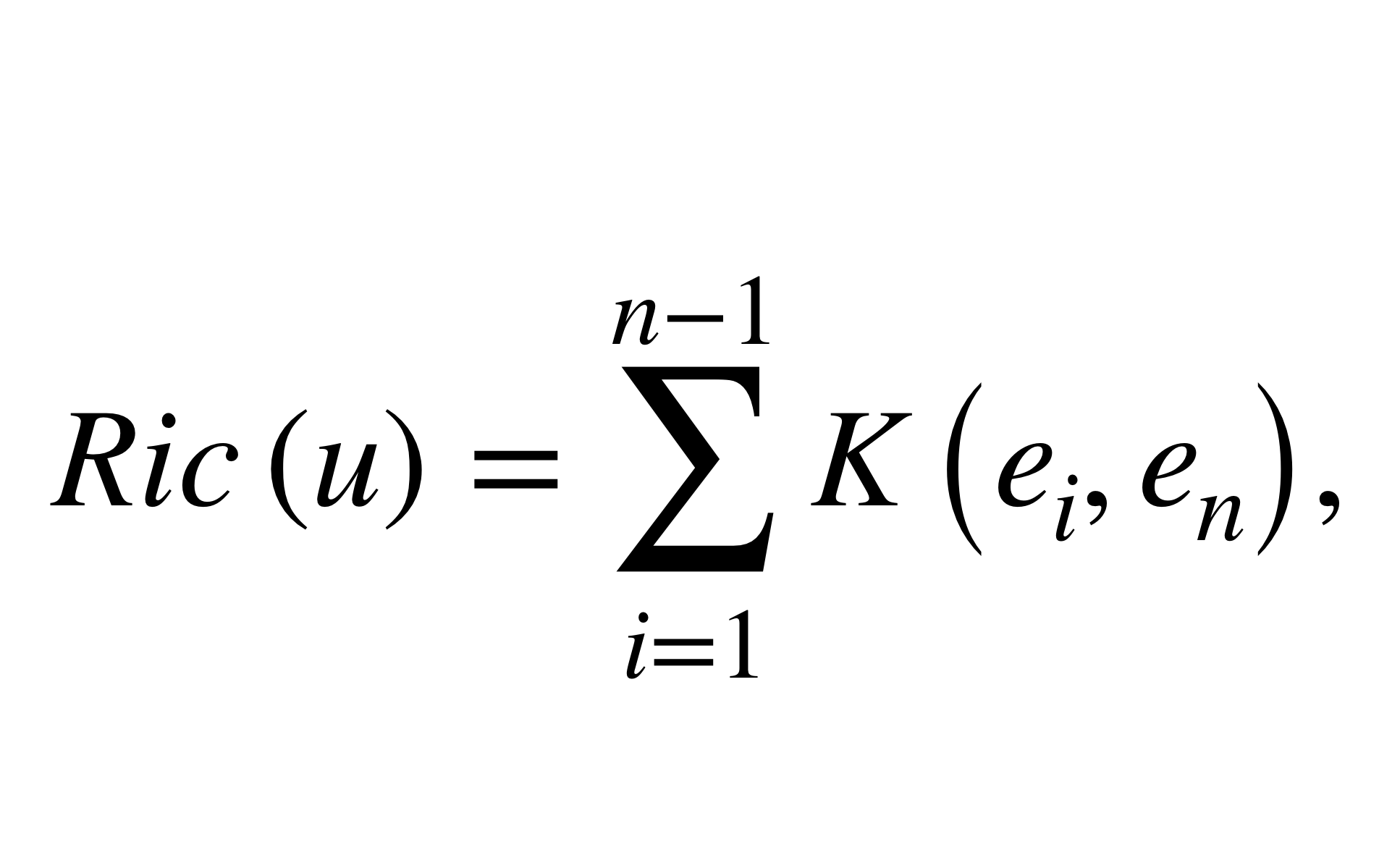
曲率是刻畫流形的重要幾何量。里奇曲率(Ricci curvature)是n維黎曼流形的n-1個截面曲率的和。
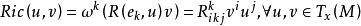
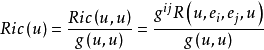

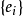
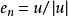
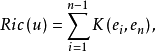
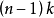

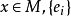

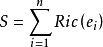

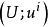
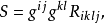
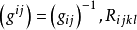
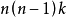

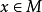
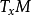
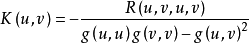
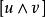
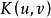
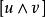

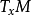
曲率是刻畫流形的重要幾何量。里奇曲率(Ricci curvature)是n維黎曼流形的n-1個截面曲率的和。...
在微分幾何中,類似度量張量,里奇張量也是一個在黎曼流形每點的切空間上的對稱雙線性形式。以格雷戈里奧·里奇-庫爾巴斯托羅(Gregorio Ricci-Curbastro)為名的里奇...
曲率張量(curvature tensor)由聯絡確定的一個重要張量。曲率張量是一個重要的數學量。在眾人所關注的廣義相對論中起到了重要的作用。沒有曲率張量,就不可能建立起...
在黎曼幾何中,數量曲率(Scalar curvature)或里奇標量(Ricci scalar)是一個黎曼流形最簡單的曲率不變數。對黎曼流形的每一點,數量曲率是由該點附近的內蘊幾何確定...
克勒-愛因斯坦度量一類特殊的克勒度量,設(M,g)是克勒流形,S為里奇曲率張量,若S滿足S=ρg,則稱g為M上的克勒-愛因斯坦度量,這時,(M,g)稱為克勒-愛因斯坦流形...
博內一邁爾斯定理(Bonnet-Myers theorem)大範圍正曲率流形的一個重要定理.設M是n維完備黎曼流形.若M的里奇曲率)(n-1)H}0,則在M上長度)耐丫萬的測地線必...
這定理說如完備黎曼流形M的里奇曲率有下界(n − 1)k > 0,那么其直徑不超過。 而且,如直徑等於 ,則流形和有常截面曲率k的球面等距。邁爾斯定理定理推廣 ...
張振雷和田剛在上述論文中解決了Fano流形上里奇曲率積分有界的凱萊-里奇流的正則性問題,在低維情況證明了有近二十年歷史的Hamilton-田剛猜想;建立了運用里奇流...
在微分幾何中,博赫納公式是將黎曼流形(M,g) 上的調和函式與里奇曲率張量聯繫在一起的公式。它以美國數學家所羅門·博赫納的名字命名。...
極小子流形的內蘊剛性是由極小子流形的內蘊曲率所描述的惟一性現象,它是極小子流形理論中的一個重要研究方向。...
熱核比較定理(comparison theorems for heatkernels)關於黎曼流形上熱核的一種估計.在對於一般黎曼流形的截面曲率或里奇曲率的適當假定下,建立黎曼流形和具有常曲率...
張振雷和田剛在上述論文中解決了Fano流形上里奇曲率積分有界的凱萊-里奇流的正則性問題,在低維情況證明了有近二十年歷史的Hamilton-田剛猜想;建立了運用里奇流...
最大直徑定理(maximal diameter theorem )是關於正曲率流形與同維球面等距的定理。...... 博內一邁爾斯定理斷言:若M的里奇曲率)(n-1)H>0,則它的直徑必鎮耐、...
