引力場是描述物體延伸到空間中對另一物體產生吸引效應的理論模型。現代觀點認為引力場是物質在空間中產生的空間彎曲效應，物體在該彎曲空間內運動時表現出在直角空間中的運動狀態改變，從而體現出引力效應。在牛頓力學的經典理論框架下和愛因斯坦的廣義相對論理論框架下均有對引力場的定量描述。然而，通過現代觀測手段發現宇宙中星際物質的運動與現有理論存在不相符的現象，因此引入了“暗物質”和“暗能量”的概念，來彌補原有理論和實際觀測的差距。儘管學術界針對暗物質和暗能量的可能的量、分布和屬性已經著手研究，但它們仍然是未知大於已知，且尚未完全證實的概念。
基本介紹
- 中文名：引力場
- 外文名：Gravitational Field
- 產生原因：暗能量和星體相互作用
- 影響地域：整個宇宙
- 代表：重力
- 特點：變化是連續的
- 屬性：空間力
簡介,動力,引力,引力簡介,引力方程,重力,向心力,萬有引力,引力強度,
簡介
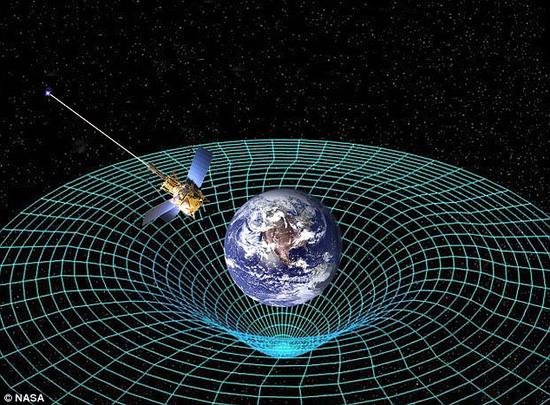
牛頓在經典力學體系中使用萬有引力定律描述物體之間的引力作用，而這種相互作用的特殊性在於僅與物體的質量和物體間距離相關。在萬有引力定律中，引力被描述為空間中任意兩個具有質量的物體之間的點對點相互作用（見引力）。而實際上，引力並不是兩個物體間實質性的吸引相互作用力，而是一個物體所具有的物理性質對另一個物體的運動產生的影響，這個物理性質同時也是一個物理量，能夠用定量的理論來進行刻畫和描述，這就是引力場理論。
在場論提出前，物理學家把粒子的相互作用看成是某種東西越過粒子之間的距離而直接作用於粒子——即所謂的超距作用。場論最先是由詹姆斯·克拉克·麥克斯韋在19世紀提出來描述電磁現象的，與之前不同的就是，場論認為作用都是局部現象，每個粒子在其自身所在地點與場發生相互作用。20世紀初阿爾伯特·愛因斯坦發展了他的引力場論，即廣義相對論。愛因斯坦認為空間是物質所具有的一種屬性，而在具有質量的物質附近，空間是彎曲的，而黎曼幾何被成功的套用於廣義相對論中，用來將彎曲的空間幾何化，並能夠將對引力場的理論描述精確定量化。廣義相對論的理論體系建立之後，科學家通過對天文現象的觀測驗證了其有效性和準確性。
就在人們認為廣義相對論已經精確的描述了我們所認知的宇宙空間時，在20世紀70年代初，科學家觀測宇宙其他一些星系中的恆星運行速度時就發現，越遠離核心的星系，其繞中心旋轉的速度並不都是衰減下去，而是具有和內圈恆星相似的速度。這個現象與越往外物質越少，引力也越小，速度也應該越低的常規不符。科學家們大膽地猜測：宇宙中一定有某些物質沒有被我們的天文觀測所發現，這些物質被稱為“暗物質”，能夠提供額外的引力場。
20世紀末，哈勃太空望遠鏡的觀測結果支持了宇宙經歷了減速膨脹到加速膨脹的階段，而這一現象在廣義相對論中對應於愛因斯坦所提出了宇宙常數不為零的情況，科學家因此提出了“暗能量”的概念，認為是這一部分能量使得廣義相對論能夠準確描述宇宙的膨脹行為。
暗物質與暗能量儘管在某種程度上彌補了廣義相對論和天文觀測之間的差距，但對它們的未知仍然遠遠大於已知，這也許是物理學和天文學進一步發展的潛在突破口。
動力
科學家們一再通過各種的觀測和計算證實，暗能量在宇宙中占主導地位，約占73%，暗物質占近23%，我們所熟悉的物質僅約占4%。所以宇宙的運動不是由我們所熟悉的物質來推動的，而是由暗能量來推動的。太陽系和銀河系的運動都是旋渦型的，所以，暗能量必定以一種旋渦運動的形式存在，以便推動它們的這種運動。結果，在暗能量運動的範圍內就會形成一種旋渦場，我們稱之為暗能量旋渦場，簡稱為旋渦場。
旋渦場存在如下三種狀態：膨脹、收縮和平衡。當太陽系旋渦場處於膨脹狀態時，所有的行星都會遠離太陽而去。當太陽系旋渦場處於收縮狀態時，所有的行星都會向太陽靠近。當太陽系旋渦場處於平衡狀態時，行星繞太陽運動的狀態就會保持不變。就這情況來看，太陽系旋渦場處於平衡狀態。在這種狀態下，太陽系的暗能量將全部轉化為太陽和行星運動的動能。換言之，太陽系的暗能量和太陽系物質運動的總動能是相等的。以En來表示太陽系的暗能量，以Ep來表示太陽系物質運動的總動能，則En=Ep。
引力
引力簡介
既然太陽系的運動是由暗能量來推動的，那么，當暗能量為零時，太陽系將失去運動的動力，它將會象一盤散沙，而不會連結成一個整體。所有的行星都不會繞太陽運動。在這種情況下，將不會存在太陽的引力，即太陽與行星之間不存在引力。所以，太陽的引力是由暗能量和太陽的質量共同產生的。由於暗能量總是以一種動能的形式出現，所以，可以用一條動能的公式來代表暗能量：En=MnVn2/2。該公式中，Vn代表暗能量的平均速度，Mn代表暗能量的虛擬質量。經此簡化，就可以認為，太陽的引力是由虛擬質量Mn和太陽的質量共同產生的。
Vn與太陽系中暗能量的分布有關，它等於4293.40米/秒。由於太陽系旋渦場處於平衡狀態，所以，En=Ep1=1640.189×108×M0焦耳，公式中，Ep1代表太陽系運動的總動能，M0代表地球的質量。詳情請看“暗能量的衰退”。把數據代入動能公式，可求得太陽系中暗能量的虛擬質量：
Mn=2En/Vn2=2×1640.189×108×M0/(4293.40)2=17796×M0
計算結果表明，太陽系中暗能量的虛擬質量是地球的17796倍。而太陽的質量卻是地球的133769倍。
引力方程
下面讓我們來建立太陽系引力場方程。用R來表示太陽系引力場中任何一點到太陽系中心的距離，用M來表示太陽的質量，用Mn代表太陽系中暗能量的虛擬質量。用F來表示太陽系引力場的引力。則可以得到如下公式：
G3=G1MnM
公式(1)中，G1是引力場的引力常數,它與萬有引力常數G的值不相同。公式(1)的意思是：太陽系引力場中某一點的引力與虛擬物質的質量Mn和太陽的質量Mp的乘積成正比，與該點到太陽系中心的距離R的平方成反比。在太陽系引力場，G1、Mn、M三者都是恆定值，G3也是一個恆定值。但對於不同的引力場，G3值是不同的。所以，公式(1)實際上就是關於引力F和距離R的關係方程式，稱之為引力場方程。相應地，我們稱G3為引力場方程的常數。
引力場中的引力與物體的質量無關。這個道理很明顯，因為引力場不是由這個物體產生的。例如，在離地面100米的A點處，不管A點處是否有物體，它都存在地球引力場的引力，而且A點處的引力值是不變的。A點處的引力並不因為物體的不存在而消失。只要地球不消失，地球引力場就會永遠存在。
當物體在旋渦場內運動時，物體的質量相對於星體來說要小到忽略不計。如果物體的質量很大，它的運動對旋渦場的動力平衡產生很大的影響，那么，旋渦場就會發生收縮或膨脹。在這種條件下，虛擬質量Mn和引力F都會發生變化，公式(1)不適用。
可以做一個實驗來檢驗公式(1)的正確性。實驗方法如下：在真空狀態下，兩個質量不同的物體處於同一高度，讓它們自由落下地面。如果它們同時到達地面，那么，就可證明自由落體到達地面所需的時間只與引力場有關，而與物體的質量無關。同時，它也證明了星體引力場的引力與物體的質量無關。
很顯然，實驗的結果是支持上述理論的，即支持旋渦場理論，也支持著萬有引力的理論
重力
物體的重力是在引力場的作用下才產生的。沒有引力場，物體就不存在重力。所以，重力不是物體本身的屬性，但它也不是引力場本身的屬性。物體本身不會產生重力，引力場本身也不會產生重力。物體的重力是引力場中和物體的質量共同作用的產物。萬有引力理論實際上把重力和引力等同了起來，它把物體的質量也當做了產生引力場的主要因素，從而分不清楚什麼是引力，什麼是重力。換言之，它無法解釋物體的重力現象。可以用如下公式來計算物體的重力：
P=G2mF …………(2)
公式(2)中，P代表物體的重力，m代表物體的質量，F代表物體在旋渦場中所處的體置的引力，G2是一個重力常數。
公式(2)的意思是：物體的重力與物體的質量和引力場的引力的乘積成正比。
重力方程
引力G1和重力G2
地球繞太陽運動的平均速度用V1來表示，它的平均軌道半徑用R1來表示。則有V1=29790米/秒,R1=1.49597870 × 1011 米,地球的質量為M0。根據地球繞太陽運動的向心力等於它的離心力的原則，可得如下公式：
R1V12 1.49597870 ×1011×(29790)21 2.209146×1010
G1G2=———=————————————=———————
MnM (17796M0)×(337691M0) M0×M0
地球的質量M0=589×1024kg,代入上式,計算後得：
G1G2=6.36786×10-38…………(4)
引力F的單位為kg/m2，它的意思是引力場中的引力是按高度的平方來遞減的。引力單位中不能有時間的單位，因為引力場中的引力與時間無關。G1的單位是kg-1,G2的單位是m3kg-1s-2。
把重力P=mg代入公式(3)後得：
G2=g/F …………(5)
引力場中的引力是一個相對概念，不是一個絕對概念。我們應該定出一種衡量引力的標準。這個標準可以按如下方法來定義：把太陽表面的引力定為274kg/m2，以此作為衡量引力場中的引力標準。太陽表面的重力加速度為274米/秒^2。根據這個標準以及公式(5),可得重力常數G2=1m3kg-1s-2。把它代入公式(4)後得：
G1=6.36786 ×10-38kg-1
向心力
以太陽係為例來說明行星的向心力。太陽系引力場中的引力可按照公式(1)來計算。行星在太陽系引力場中的重力P可按公式(2)來計算。把公式(1)代入公式(2)，可得如下公式：
P=G2mF= 
…………(3)
萬有引力
科學家們可以用萬有引力公式來計算地球繞太陽運動的向心力，其計算結果用F0來表示。也可以用上述公式(3)來計算地球繞太陽運動的向心力，其計算結果用P0來表示。通過比較會發現，F0=P0。為什麼兩種不同的理論會有相同的結果？原因很簡單：理論上的不完善往往可以用公式中的常數來修正。因為這種常數是科學家們通過大量實驗和計算得出來的結果，是正確的。
在同一個引力場中，如在太陽系引力場中，萬有引力常數G是一個恆定值。但在不同的引力場中，G值是不相同的。當暗能量發生變化時，G值也會發生變化。
結論：公式是對的並不等於它的理論是完全對的。
引力強度
根據萬有引力定律（平方反比定律），引力場強度是描述引力場的性質的基本物理量，是個矢量。它與電場強度完全等效。
在引力場中某觀察點的引力場強度E，等於置於該點的靜止質點m所受的引力力F與質量m的比。
引力場強度的單位應是牛(頓)每千克。在國際單位制中，符號為N/kg。如果1kg的質點在引力場中的某點受到的萬有引力是1N，這點的引力場強度就是1N/kg。如果拿地球表面為研究對象，它的引力場強度則為g，即重力加速度大小。但是，引力場強度並不等於加速度。
廣義相對論中，引力場被描述為因質量而彎曲的時空，因此引力場的“強度”可以用方程左邊的度規張量描述。度規張量唯一確定了時空的幾何性質。對於閔可夫斯基時空（沒有引力的時空，即狹義相對論研究的四維時空），度規g（11）=-c^2, g（22）= g（33）=g（44）=1，其餘g（ij）=0。
