質點作曲線運動時,指向圓心(曲率中心)的加速度,與曲線切線方向垂直,也叫做法向加速度。向心加速度是反映圓周運動速度方向變化快慢的物理量。向心加速度只改變速度的方向,不改變速度的大小。
基本介紹
- 中文名:向心加速度
- 外文名:centripetal acceleration
- 套用領域:經典力學
- 屬性:可能是實際加速度或分加速度
- 適用情況:圓周運動
公式,方向,思維誤區,問題解析,
公式
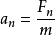
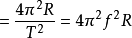
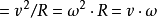
上式中,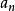 表示向心加速度,
表示向心加速度, 表示向心力,
表示向心力,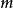 表示物體質量,
表示物體質量, 表示物體圓周運動的線速度(切向速度),
表示物體圓周運動的線速度(切向速度),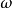 表示物體圓周運動的角速度,
表示物體圓周運動的角速度,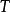 表示物體圓周運動的周期,
表示物體圓周運動的周期,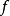 表示物體圓周運動的頻率,
表示物體圓周運動的頻率,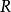 表示物體圓周運動的半徑。(
表示物體圓周運動的半徑。(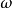 =2π/T)
=2π/T)
由牛頓第二定律,力的作用會使物體產生一個加速度。合外力提供向心力,向心力產生的加速度就是向心加速度。可能是實際加速度,也可能是物體實際加速度的一個分加速度。
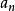

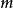

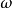
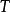
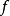
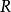
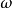
由牛頓第二定律,力的作用會使物體產生一個加速度。合外力提供向心力,向心力產生的加速度就是向心加速度。可能是實際加速度,也可能是物體實際加速度的一個分加速度。
方向
方向始終與運動方向垂直,方向時刻改變且指向圓心(曲率中心),不論加速度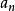 的大小是否變化,
的大小是否變化,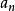 的方向是時刻改變的,所以圓周運動一定是變加速運動。可理解為做圓周運動物體加速度在指向圓心(曲率中心)方向上的分量。
的方向是時刻改變的,所以圓周運動一定是變加速運動。可理解為做圓周運動物體加速度在指向圓心(曲率中心)方向上的分量。
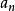
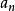
向心加速度是矢量,並且它的方向無時無刻不在改變且指向圓心(曲率中心)。
所有做曲線運動的物體都有向心加速度,向心加速度反映的是圓周運動在半徑方向上的速度方向(即徑向即時速度方向·)改變的快慢。
當物體的速度大小也發生變化時,還有沿軌跡切線方向也有加速度,叫做切向加速度。
向心加速度的方向始終與速度方向垂直,也就是說線速度始終沿曲線切線方向。
思維誤區
②據公式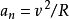 ,誤認為
,誤認為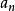 與
與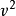 成正比,與半徑
成正比,與半徑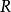 成反比。事實上,只有在半徑
成反比。事實上,只有在半徑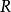 確定時才能判斷
確定時才能判斷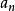 與
與 或
或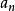 與
與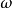 的關係。
的關係。
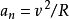
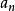
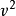
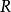
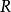
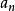

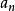
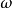
③向心加速度的公式也適用於非勻速圓周運動,且無論是勻速圓周運動還是非勻速圓周運動,向心加速的的方向都指向圓心。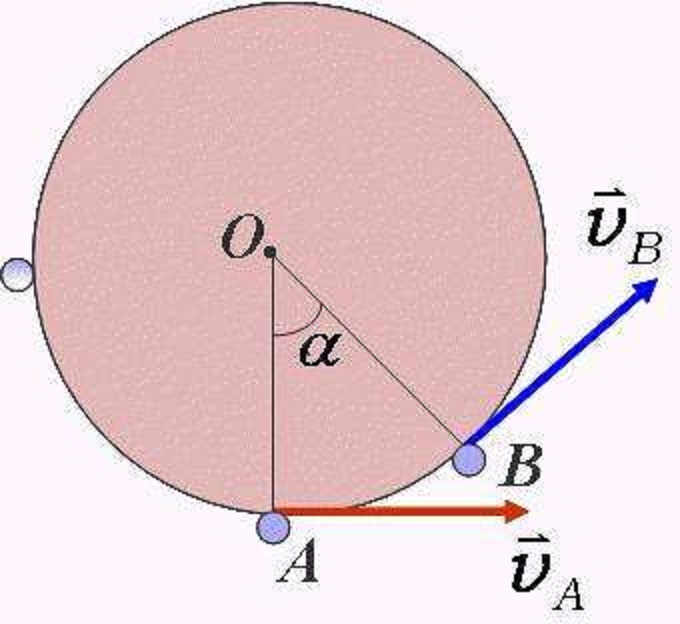

問題解析
通過下面兩個問題的探討和解析,可進一步鞏固和深化學生對勻速圓周運動的認識和理解。
1.向心加速度表征什麼意義?
要弄清這個問題,首先要明確矢量三角形中△v的物理意義(圖4)
它只表 示速度方向的改變,而不表示速度大小的改變,故而向心加速度所表征的僅僅是速度方向變化的快慢。
2.做勻速圓周運動的物體是否“落”向圓心?
這個問題寓知識於趣味之中,很值得提出來與學生一起探討,如圖5所示,若物體在a點不再具有加速度aa,則物體必將沿ae方向飛出,經t秒後到達e點,而如今物體卻“落”到b點上,即離開了ae一段距離eb.當時間t取得足夠短時,b點和a點非常接近,且以a點為極限,則可認為ab弧和ab弦互相重合,eb和ad互相重合,且有ab弦=vt,eb=ad.因rt△abc∽rt△adb,則ad/ab=ab/ac,即
由此可見,物體確是時時“落”向圓心,只不過並不能真的到達圓心而已。顯然,這是向心加速度導致的結果。
向心加速度公式證明方法(2)並附圖
又如圖丁(圓O的一部分,即扇形,OQ=OP=r,同時有弦PQ和弧PQ),設θ為OQ與OP夾角的弧度數(其實是數學上這個角對應的弧長與圓半徑的比值,即弧PQ :半徑r的值,如一弧度≈57.3°)那么我們知道 X·Y/X=Y,則弧PQ的長度可以表示為“半徑r·弧PQ/半徑r”即弧長=半徑×對應弧度。 當夾角θ很小很小時,可近似認為弧PQ=弦PQ,也就是說彎曲的弧長與筆直的線段長度幾乎一樣,這就為後面的求△V提供了依據。
回到圖乙,如圖當OB,OA之間的夾角(等於Vb與Va的夾角)很小很小時,那么對應的△V就很小很小了,並且以B為頂點,母線長為Va(或Vb)的扇形中由A點到B點所掃過的弧△V就可近似等於弦△V,即根據圖丁作介紹的,若把圖丁中的半徑r看做線速度Va(或Vb),弧長=半徑×對應弧度(也就是先前的V=ω·r)用在圖乙中就是弧△V=△V=線速度(視為半徑r)×弧度θ(弧△V與可視為圓半徑r的線速度Va或Vb的比值)
而當△V這個量小到單位時(即一秒鐘內△V的量),那么這個△V就是我們所說的向心加速度a,向心加速度a=△V/△t,而弧△V=弦△V,所以向心加速度a=弧△V/△t。
首先弧度θ是質點經過某一時間(△t)做圓周運動所轉過的角度的弧度數,則角速度ω=θ/△t,表示一秒鐘內轉過的弧度數,即弧度θ=ω·△t,①並且△V=弧△V=向心加速度a×△t。②
再根據弧長=半徑×對應弧度,弧△V=△V=線速度V×弧度θ(如圖丙,當θ小到一定程度時,弧△V=△V,小到單位弧度時就存在這樣的關係)再根據①②兩式,得出向心加速度a×△t=線速度V(這個矢量的大小始終不變)×角速度ω·△t,同時除去等式左右的△t,於是最終化簡為:
向心加速度a=角速度ω×線速度V,即a(n)=ω·V,還有a(n)=ω2·r,a(n)=V^2/r等等 都是根據此式以及V=ω·r推理出來的。

 證明方法(2)的圖片
證明方法(2)的圖片