基本介紹
概述
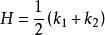
定義
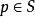
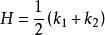

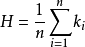
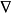
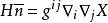
三維空間中曲面
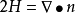
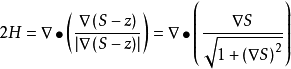
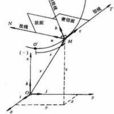
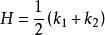
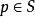
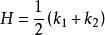

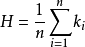
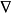
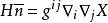
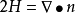
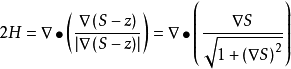
平均曲率(mean curvature) 是微分幾何中一個“外在的”彎曲測量標準,局部地描述了一個曲面嵌入周圍空間(比如二維曲面嵌入三維歐幾里得空間)的曲率。平均曲率是空間上...
全平均曲率(total mean curvature)表征曲面整體性質的一個重要外在概念。...... 全平均曲率(total mean curvature)表征曲面整體性質的一個重要外在概念。...
曲線的曲率(curvature)就是針對曲線上某個點的切線方向角對弧長的轉動率,通過微分來定義,表明曲線偏離直線的程度。數學上表明曲線在某一點的彎曲程度的數值。曲率越...
常平均曲率曲面(surfaces with constant meancurvature)一類重要的曲面,它是平均曲率H為常數的曲面。...
指定平均曲率方程(prescribedmean curvatureequation)平均曲率為已知的曲面所滿足的方程...
過曲面上某個點上具有無窮個正交曲率,其中存在一條曲線使得該曲線的曲率為極大,這個曲率為極大值Kmax ,垂直於極大曲率面的曲率為極小值Kmin。這兩個曲率屬性...
常曲率曲面有常高斯曲率曲面和常平均曲率曲面。一般常曲率曲面指的是常高斯曲率曲面。一個高斯曲率在各點上均取相同值的曲面,我們稱這曲面為常高斯曲率的曲面。...
絕對全曲率是表征曲面整體性質的一個重要內蘊概念。絕對全曲率的概念已被陳省身、拉肖夫(Lashof,R.K.)等推廣到高維子流形上。...
仿射主曲率(affine principal curvature)刻畫仿射空間中超曲面彎曲程度的不變數.它是歐氏曲面論中主曲率的仿射類似.設M是n+1維仿射空間中的局部嚴格凸的超曲面,二...
曲率張量(curvature tensor)由聯絡確定的一個重要張量。曲率張量是一個重要的數學量。在眾人所關注的廣義相對論中起到了重要的作用。沒有曲率張量,就不可能建立起...
構造主曲率法是指使用趨勢面分析與差分法相結合的方法,處理離散的構造層面數據,計算構造面主曲率,選取各點主方向上兩個主曲率值中絕對值較大者作為裂縫發育區...
在黎曼幾何中,復曲率(或Ricci標量)是黎曼流形的最簡單的曲率不變數。 對於黎曼流形的每個點,它分配由該點附近的歧管的固有幾何確定的單個實數。 具體來說,復...
如此類推,如果里奇曲率在給定的向量 的方向是負的,流形同樣的圓錐區域的體積比歐幾里得空間對應的圓錐區域要大。里奇曲率本質上就是包含 的平面的曲率平均。也就...
角膜曲率儀測定角膜前表面曲率可為選擇合適的軟性角膜接觸鏡基弧提供依據,也可通過角膜曲率儀檢查了解角膜散光度,為驗光提供參考依據。...
撰有論文《芬斯勒流空間的子空間的平均曲率》、《黎曼曲面》、《凸區域的一個遮蓋定理》,著有《現代分析基礎》。張鳴鏞經歷 編輯 ...
在數學中,極小曲面是指平均曲率為零的曲面。舉例來說,滿足某些約束條件的面積最小的曲面。 物理學中,由最小化面積而得到的極小曲面的實例可以是沾了肥皂液後吹...
