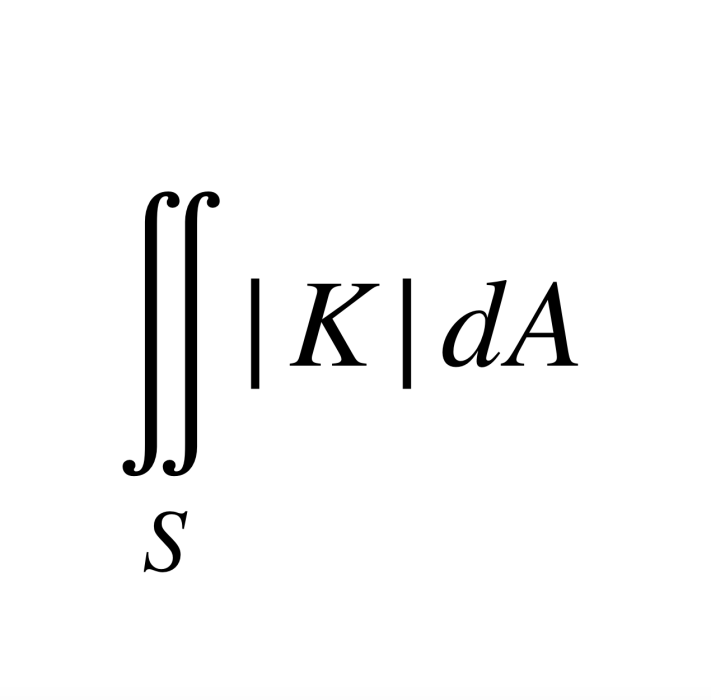絕對全曲率

絕對全曲率是表征曲面整體性質的一個重要內蘊概念。絕對全曲率的概念已被陳省身、拉肖夫(Lashof,R.K.)等推廣到高維子流形上。

基本介紹

• 中文名：絕對全曲率
• 外文名：total absolute curvature
• 適用範圍：數理科學

簡介

絕對全曲率是表征曲面整體性質的一個重要內蘊概念。

設 S 是 R中的緊緻連通閉曲面，K 是它的高斯曲率，積分

稱為曲面 S 的絕對全曲率，這裡 dA 是曲面 S 的面積元素。

曲面的絕對全曲率

曲面的絕對全曲率滿足不等式

這裡 χ 是曲面歐拉一龐加萊示性數，式中等號若且唯若 S 是卵形面時成立。

絕對全曲率的概念已被陳省身、拉肖夫(Lashof,R.K.)等推廣到高維子流形上。

全平均曲率

(total mean curvature)

全平均曲率是表征曲面整體性質的一個重要外在概念。

設 S 是 R 中的緊緻連通閉曲面，它的平均曲率為 H ，積分

稱為曲面S的全平均曲率，這裡 dA 是曲面 S 的面積元素。

它是由威爾莫(Willmore,T. J.)於1965年首先提出的。