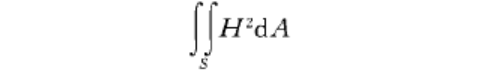
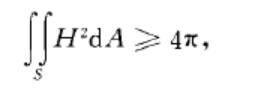
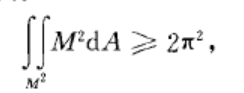
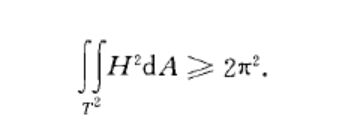
全平均曲率(total mean curvature)表征曲面整體性質的一個重要外在概念。
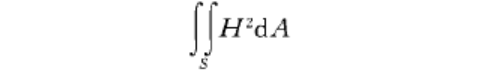
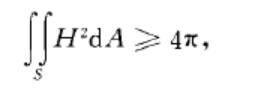
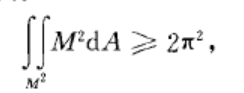
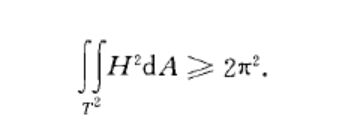
全平均曲率(total mean curvature)表征曲面整體性質的一個重要外在概念。全平均曲率(total mean curvature)表征曲面整體性質的一個重要外在概念.設S是R3中的緊緻...
1 簡介 2 曲面的絕對全曲率 3 全平均曲率 絕對全曲率簡介 編輯 絕對全曲率是表征曲面整體性質的一個重要內蘊概念。設S 是 R3中的緊緻連通閉曲面,K 是它的...
平均曲率(mean curvature) 是微分幾何中一個“外在的”彎曲測量標準,局部地描述了一個曲面嵌入周圍空間(比如二維曲面嵌入三維歐幾里得空間)的曲率。 平均曲率是空間...
常平均曲率曲面(surfaces with constant meancurvature)一類重要的曲面,它是平均曲率H為常數的曲面。例如,球面是常平均曲率曲面.此外,將一橢圓在其平面內一條定直線...
弧 的切線轉角 與該弧長 之比的絕對值稱作該弧的平均曲率,記作當 沿曲線L趨向於M時,若弧 的平均曲率的極限存在,則稱此極限為曲線L在點M處的曲率,記作K,...
平均曲率、主曲率和高斯曲率是曲率的三個基本要素。主曲率主曲率和主方向 編輯 對曲面S : r = r(u, v)上一給定點P0(u0, v0),法曲率kn是切方向du : ...
指定平均曲率方程(prescribedmean curvatureequation)平均曲率為已知的曲面所滿足的方程.如果Rn+’中的曲面xn+i=u}x)}x=}x,}xZ,...,,x,})E ,f2的平均曲率...
常平均曲率曲面(surfaces with constant mean curvature)是一類重要的曲面,它是平均曲率H為常數的曲面。例如,球面是常平均曲率曲面,此外,將一橢圓在其平面內一條定...
1. 平均擴散率 .術語線上[引用日期2020-08-09] 學術論文 內容來自 朱春香. 平均曲率運動與非線性擴散方程的數值方法和套用研究. 《 西北大學 》 , 年 查...
在數學中,極小曲面是指平均曲率為零的曲面。舉例來說,滿足某些約束條件的面積最小的曲面。 物理學中,由最小化面積而得到的極小曲面的實例可以是沾了肥皂液後吹...
全臍點子流形(totally umbilical submanifold) [1] 一類子流形.第二基本形式與第一基本形式只差一個平均曲率向量因子的子流形.
