基本介紹
- 中文名:極小曲面
- 外文名:minimal surface
- 學科:數理科學
- 套用領域:計算機仿真,建築設計
簡介
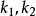
 圖1.極小曲面的例子
圖1.極小曲面的例子定義


與布朗過程的聯繫
相關研究
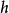
 圖2.極小曲面
圖2.極小曲面
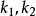
 圖1.極小曲面的例子
圖1.極小曲面的例子

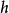
 圖2.極小曲面
圖2.極小曲面在數學中,極小曲面是指平均曲率為零的曲面。舉例來說,滿足某些約束條件的面積最小的曲面。 物理學中,由最小化面積而得到的極小曲面的實例可以是沾了肥皂液後吹...
《極小曲面》是2011年大連理工大學出版社出版的圖書,作者是陳維桓。陳維桓所著的《極小曲面》的目的是介紹3維歐氏空間中極小曲面的概念、典型例子和性質,以及一些...
《極小曲面 (平裝)》是出版圖書,作者是吳光磊...... 本書從肥皂膜的實驗入手,以淺顯易懂的語言深入淺出地介紹了3維歐式空間中極小曲面的概念、典型例子和性質,...
射影極小曲面(projective minimal surface)是射影曲面論的基本元素之一。這個定義是湯姆森(Thomson,G.)於1928年給出的。射影極小曲面有許多特徵。...
極小子流形是一類平均曲率向量為0的子流形。極小子流形是整體微分幾何的重要課題。它與微分方程、拓撲學、幾何測度論、複變函數論等數學分支都有緊密的聯繫,並...
那么X就稱為一般型極小曲面。嚴格地講, 一般型極小曲面就是指小平維數kod(X)=2的極小代數曲面。一般型曲面背景 編輯 代數曲面分類,是經典代數幾何最重要的...
螺旋曲面可視為一個線段沿著垂直於其中點的直線,勻速螺旋上升時掃過的曲面,可視為是螺旋線的立體版本,是在平面及懸鏈曲面後,第三個已知的極小曲面。螺旋曲面曾在...
道格拉斯泛函是道格拉斯(Douglas,J.)為解決極小曲面問題引進的一個泛函。...... 道格拉斯泛函是道格拉斯(Douglas,J.)為解決極小曲面問題引進的一個泛函。...
在空間內以給定的閉曲線為邊緣張以肥皂膜時,表面張力使膜穩定在表面積為最小的狀態。這刺激了科學家對極小曲面的研究。因此,極小曲面問題又稱為普拉托問題。...
吉敏,女,江蘇省海安縣人,1960年出生。研究方向:偏微分方程。吉敏教授主要從事偏微分方程理論的研究,特別是具幾何、物理背景的非線性微分方程。例如,流形上的極小...
正螺面(circular helicoid),即正螺旋面,是一種特殊的曲面。它是直紋極小曲面,即一曲線C繞直線 l 以定角速度旋轉,同時沿直線 l 的方向等速移動所生成的曲面。...
懸鏈面(catenoid)是一種特殊的曲面,是微分幾何中很重要的一種曲面,它是旋轉極小曲面。懸鏈線指兩端固定的一條(粗細與質量分布)均勻、柔軟(不能伸長)的鏈條,在...
一個曲面是極小曲面若且唯若平均曲率為零。此外,平面 S 平均曲率滿足一個熱型方程稱為平均曲率流方程。平均曲率三維空間中曲面 編輯 對3 維空間中的曲面,平均...
丘成桐與Meeks 合作解決了三維流形極小曲面一個著名的問題,即一條極值約當曲線的極小圓盤的Plateau 問題的Douglas 解,當邊界曲線是一個凸邊界的子集,那么它在三維...
另外,施瓦茨與魏爾斯特拉斯一道深入地研究了微分幾何中極小曲面問題,他們認為這個問題與複變函數、變分學、拓撲學都有很深的關係。...
(1) 陳文財,黎鎮琦,偽球面上的常負曲率極小曲面,南昌大學學報,2001,3(2) 陳文財,黎鎮琦,偽球面上的常正曲率類空極小球面,數學年刊,2003,2...
丁偉岳的研究領域包括常微分方程,半線性橢圓形方程,調和映射和極小曲面,預定數量曲率問題,Schrodinger流,復幾何中的Kahler-Einstein度量存在性等 [3] 。中文...
變分法是17世紀末發展起來的一門數學分支,是處理函式的數學領域,和處理數的函式的普通微積分相對。它最終尋求的是極值函式:它們使得泛函取得極大或極小值。變分...
主要研究方向是微分幾何及其在數學物理中的套用,主要研究調和映射與可積系統、調和映射的幾何、子流形的幾何與分析(特別對稱空間中的極小曲面的幾何與分析)等。...
曲線的解析幾何,曲線和曲面的微分幾何之類的一般幾何外,它還包括了共形映射、極小曲面、數的幾何及其在數論中令人驚奇的套用、位形空間之幾何、多面體與曲面的拓撲...
對黎曼曲面及其模空間的動力學和幾何作出了突出的貢獻 37 2018 皮特·舒爾茲 ...考切爾·比爾卡爾 伊朗 證明了法諾代數簇的有界性以及對極小模型理論的貢獻 40...
