射影極小曲面(projective minimal surface)是射影曲面論的基本元素之一。這個定義是湯姆森(Thomson,G.)於1928年給出的。射影極小曲面有許多特徵。
基本介紹
- 中文名:射影極小曲面
- 外文名:projective minimal surface
- 領域:數學
- 學科:射影曲面論
- 性質:變分問題的解曲面
- 提出者:湯姆森
概念
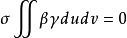
射影微分
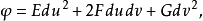

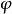
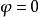
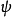
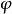
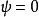
共軛網

射影極小曲面(projective minimal surface)是射影曲面論的基本元素之一。這個定義是湯姆森(Thomson,G.)於1928年給出的。射影極小曲面有許多特徵。
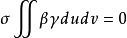
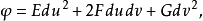

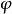
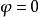
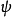
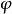
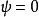

射影極小曲面(projective minimal surface)是射影曲面論的基本元素之一。這個定義是湯姆森(Thomson,G.)於1928年給出的。射影極小曲面有許多特徵。...
設X是射影代數曲面, 如果X不包含(-1)-曲線, 並且它的第一陳類c_1(X) 以及結構層 O_X 的上同調 示性類χ(O_X),分別滿足:c_1^2(X)>0, χ(O_...
《射影曲面概論》 科學出版社出版,是著者繼《射影曲線概論》後的又一本射影微分幾何專著,概括了作者在1935年左右和近年來在這方面的研究成果...
射影極小曲面的杜慕蘭變換(Ⅳ)[J]. 數學學報,1958,(02):239-242. 4. 朱玉峻,王玲書,張金蓮. 具有雙曲不變集系統的極限跟蹤性[J]. 數學年刊A輯(中文...
還論述了仿射極小曲面,曲線、曲面的大範圍性質等問題,其方法同射影微分幾何學的富比尼方法相類似,分別使用了自然方程和基本微分形式,從而導出空間曲線和曲面論的基本...
推廣了Donaldson 關於射影代數曲面,以及Narasimhan 和Seshadri 關於代數曲線的結果...丘成桐與Meeks 合作解決了三維流形極小曲面一個著名的問題,即一條極值約當曲線...
如仿射曲面論中的錐面、射影曲線的一般的協變理論、射影曲面論中的Q1伴隨曲面、主切曲線屬於一個線性叢的曲面、射影極小曲面和閉拉普拉斯序列等方面的研究,得到...
回答也是肯定的,即:除了有一族漸近曲線屬於線形叢外,還存在且只存在一種特殊的射影極小曲面(projective minimal surfaces of concidence),它的一族漸近曲線是互相...
1.3 具有平面仿射曲率線的仿射極小曲面 1.4 在情況1o下的曲面 1.5 在情況...特別是它與射影微分幾何的關係並不那么清晰易見,這兩方面的遺留問題成了20年代...
在射影空間中,給定一個非退化的二階曲面∑,空間中每一點P都有一個確定的極面,對於空間中的一個點列,其對應的極面構成一個平面束,這個平面束的軸與點列的...
射影幾何學 微分幾何學 曲面的基本形式 極小曲面 黎曼幾何學 黎曼流形 微分流形 廣義相對論的產生及其對幾何學的影響 三、數論與代數學 數論 代數數論 代數...
射影幾何學微分幾何學曲面的基本形式極小曲面黎曼幾何學黎曼流形微分流形廣義相對論的產生及其對幾何學的影響三、數論與代數學數論代數數論...
