譜表示定理(spectral representation theorem)是平穩隨機過程相關函式的頻域表達。統計特性在不同時刻平穩不變的一類隨機過程。數學上嚴格的平穩性概念是:一隨機過程,如兩組時刻狀態變數的聯合機率密度函式是完全相同的,稱為平穩隨機過程。
基本介紹
- 中文名:譜表示定理
- 外文名:spectral representation theorem
- 領域:數學
- 過程:平穩隨機過程
- 性質:頻域表達方式
- 相關定理:譜分解定理
概念,平穩隨機過程,相關函式,譜密度,
概念
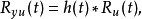


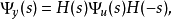
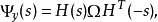
這裡H(s)是一個正的實有理傳遞函式,其所有的極點均在左半開複平面;

H(s)所有的極點均在左半開複平面或在jω軸上;Ω=Ω>0是實矩陣。若對所有滿足Re(s)=0的s還有|Φy(s)|≠0,則H(s)的所有極點均在左半開複平面。根據(4)和譜分解定理,當輸入是譜密度為Ω的白噪聲時,過程y(t)可看成是穩定系統H(s)的輸出,這就是譜表示定理。譜密度、譜分解定理等可用於線性隨機系統。
平穩隨機過程
統計特性在不同時刻平穩不變的一類隨機過程。數學上嚴格的平穩性概念是:一隨機過程,如兩組時刻狀態變數X(t1),X(t2),…,X(tn)和X(t+t1),X(t+t2),…,X(t+tn)的聯合機率密度函式f(x(t1),x(t2),…,x(tn))與f(x(t+t1),x(t+t2),…,x(t+tn))是完全相同的(對所有的t和n),稱為平穩隨機過程。一般只要求隨機變數的均值和方差的平穩性,而不要求密度函式完全相等,對均值和方差保持平穩的過程,稱為弱平穩隨機過程或廣義平穩隨機過程。對水文現象,當在一定時期內,氣候條件沒有明顯改變,流域狀況和人類活動基本穩定,就認為河川年徑流量和年最大洪峰流量等水文變數的變化屬於平穩隨機過程,不同時段觀測序列求得的各種統計特徵基本上是一致的。
相關函式
二階矩過程的重要數量特徵。設{X(t),t∈T}是一個二階矩過程,定義在T×T上的二元函式R(s,t)=E(X(s)·)稱為該過程的相關函式。
相關函式具有如下性質:
1.R(t,t)≥0,對所有t∈T.
2.對稱性.R(s,t)=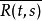 ,對所有s,t∈T.
,對所有s,t∈T.
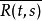
3.非負定性.對任意正整數n,t1,t2,…,tn∈T及任意複數λ1,λ2,…,λn,有:
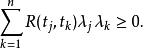
譜密度
譜密度是指當信號的頻頻寬度趨近於零時,每單位頻寬的均方根值。單位是μPa 。應當注意,譜密度只適用於具有連續譜的信號,信號的種類必須指明,例如聲壓、質點速度、質點加速度等。
在套用數學和物理學中,譜密度、功率譜密度和能量譜密度是一個用於信號的通用概念,它表示每赫茲的功率、每赫茲的能量這樣的物理量綱。
儘管並非一定要為信號或者它的變數賦予一定的物理量綱,下面的討論中假設信號在時域內變化。
