共軛直線(conjugate lines)是指成對出現的兩條直線。群中一種重要的等價關係。設S,T是群G的兩個非空子集,H是G的子群,若存在H中元素g使得T=g-1Sg=Sg,則稱S和T關於H共軛,其中T=g-1Sg={g1sg|s∈S}稱為S按g的變形。
基本介紹
- 中文名:共軛直線
- 外文名:conjugate lines
- 領域:數學
- 定義:成對出現的兩條直線
- 空間:射影空間
- 性質:共軛
概念,二階曲面,二次曲面,射影空間,共軛,
概念
共軛直線(conjugate lines)是指成對出現的兩條直線。在射影空間中,給定一個非退化的二階曲面∑,空間中每一點P都有一個確定的極面,對於空間中的一個點列,其對應的極面構成一個平面束,這個平面束的軸與點列的底稱為關於二階曲面∑的一對共軛直線。
二階曲面
二階曲面是空間射影幾何研究的基本對象。設空間中點的齊次坐標或射影坐標為(x1,x2,x3,x4),則滿足四元二次齊次方程:
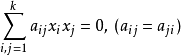
二次曲面
三維歐幾里得空間裡坐標x、y、z之間的二次方程:
ax2+by2+cz2+2fyz+2gzx+2hxy+2ux+2vy+2wz+d=0
(係數a,b,c,…為實數,二次項係數不全為零)表示的曲面。早在公元前3世紀,古希臘數學家阿基米德就寫過一本《論球和圓柱》的論著,從幾個定義和公理出發,推出關於球與圓柱的面積及體積等50多個命題。阿基米德、阿波羅尼奧斯、海倫等人還研究過拋物鏡面的反射問題,這是早期對一些特殊二次曲面的探討,其中被研究的還有雙葉雙曲面和橢球面,都是由圓錐截線繞軸旋轉產生的曲面。
解析幾何建立後,二次曲面研究在理論上有較大進展。1731年法國數學家克萊羅給出某些二次曲面的求積公式,並指出x、y、z的齊次方程表示頂點在原點的一個錐面。1748年大數學家歐拉在他的《無窮分析引論》中研究了三個變數的一般二次方程,得到6種二次曲面:錐面、柱面、橢球面、單葉和雙葉雙曲面、雙曲拋物面以及拋物柱面,並主張按方程的次數將二次曲面進行分類,認為次數是線性變換下的不變數。1802年法國幾何學家蒙日及其學生證明了二次曲面的每一個平面截口是一條二次曲線,且平行截面截得的是相似的二次曲線。1832年瑞士數學家施泰納用射影幾何的方法構造了直紋二次曲面理論,到今天已日臻完善,成為解析幾何學的重要組成部分。
射影空間
整體幾何最基本的研究對象之一。射影空間的概念最初產生於古典射影幾何。對於射影定理中的奇異情形(即有些直線相互平行的情形),為方便起見引入無窮遠點的概念,即規定平面上每條直線上有一個無窮遠點,兩條直線平行就是相交於無窮遠點,所有無窮遠點組成一條無窮遠直線。這種構造方法還可以推廣到高維空間,建立n維(實)射影空間PR。在n維射影空間中常採用齊次坐標(X0∶X1∶…∶Xn),其中X0,X1,…,Xn不全為0;若a≠0,則(aX0∶aX1∶…∶aXn)與(X0∶X1∶…∶Xn)表示同一個點。因此n維(實)射影空間同構於(Rn+1-{0})/R。進一步的研究表明PR是緊緻解析流形。若令Ui(0≤i≤n)為PR中坐標Xi≠0的點全體,則UiR,且U0,U1,…,Un組成PR的一個開覆蓋。上述構造方法可以推廣到任意體K上,建立K上的n維射影空間PK。在概形理論中,還將射影空間建立在整數環Z上,即建立射影概形PZ。由此對任意概形X可以建立PX,它是X和PZ(在Spec Z上)的纖維積。特別地,若X=Spec K(K為域),則PX=PK。
由於射影空間的性質非常豐富難以全面列舉,僅舉數例如下:
1.P1R同胚於圓,P1C可看做添上無窮遠點的複平面,同胚於球面。
2.P2R是單側曲面,可以同胚地嵌入四維空間R4,但不能同胚地嵌入三維空間R3,P2C是代數極小曲面。
3.PnC是克勒流形,它的閉解析子空間都是代數的。
4.對任意域k,Pnk是齊性空間,其切叢由整體向量場生成,其自同構群為射影群PSL(n+1,k),其皮卡群Pic(Pk)Z。
共軛
群中一種重要的等價關係。設S,T是群G的兩個非空子集,H是G的子群,若存在H中元素g使得T=g-1Sg=Sg,則稱S和T關於H共軛,其中T=g-1Sg={g1sg|s∈S}稱為S按g的變形。若S為G的子群,T稱為S關於H的共軛子群;若S={s}為一個元的集合,則稱t=g-1sg為s關於H的共軛元。當H=G時,通常就不加“關於G”這個修飾詞了。共軛關係是一種等價關係。設S是群G的一個子集,H是G的一個子群,與S關於H共軛的所有子集組成的集合稱為S關於H的共軛類。當S={s}為一個元素的集合,s關於G的共軛類是元素的集合,就簡稱G(的元素)的一個共軛類。
