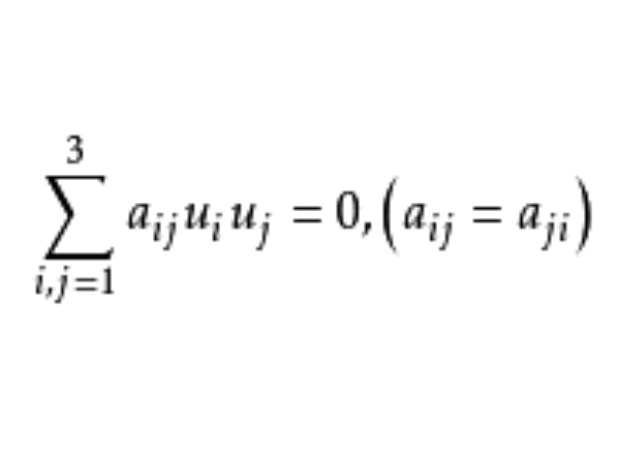二級曲線

二級曲線(two class curve)是二次曲線的一種表示方法，即用線坐標表示的二次曲線。當直線ux+vy+w=0的係數u，v，w滿足實係數二次方程Au²+2Huv+Bv²+2Guw+2Fvw+Cw²=0(式中(A，B，H)≠(0，0，0))時，這些直線的包絡線稱為二級曲線，它與二次曲線在本質上是一樣的。

基本介紹

• 中文名：二級曲線
• 外文名：two class curve
• 所屬學科：數學
• 所屬問題：平面解析幾何(圓錐曲線)
• 簡介：用線坐標表示的二次曲線

基本概念

二級曲線(two class curve)是平面射影幾何研究的基本對象，若平面上直線的齊次坐標為[u₁，u₂，u₃]，則滿足三元二次齊次方程

的直線的全體稱為二級曲線。這裡a_ij為實數且至少有一個不是零，該方程稱為二級曲線的方程，(a_ij)稱為係數矩陣。若係數矩陣的行列式|a_ij|≠0，則二級曲線稱為非退化的，否則稱為退化的、退化的二級曲線是兩個點。在射影平面上，成射影對應的兩個點列對應點的連線的集合是二級曲線。

二級曲線的方程

在射影平面上，配極變換的自共軛直線的集合稱為二級曲線。

對於給定的配極變換，即

其中 是在 中 的代數餘子式。易得 對應的二級曲線的方程。

配極 對應的二階曲線 的方程是

就是

若 是雙曲型的，則它有無窮多條自共軛直線，於是雙曲型配極對應的二級曲線有無窮多實直線，有時也將它稱為二次線束，見圖1。

圖1

若 是橢圓型的，則它無自共軛直線，於是橢圓型配極對應的二級曲線不存在，或說對應虛二級曲線。

通過矩陣，配極變換與二階曲線(或二級曲線)有著一種對應關係：雙曲型配極對應實曲線；橢圓型配極對應虛曲線。因此，可以從有關配極的一些概念出發，通過“翻譯”，建立有關曲線的對應概念。不過，人們常常關心的是有實圖形存在的情況，因此，我們只就雙曲型配極對應的曲線討論之。

對於雙曲型配極 對應的二級曲線 ，就一點與 的關係而言，有以下三類：

1.切點： 的自共軛點稱為 的切點，切線就是過該點的自共軛直線，如圖2中的點a；

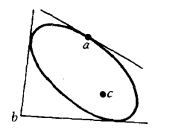圖2

2.二切線點：有二自共軛直線通過的點稱為 的二切線點，如圖2中的點b；

3. 無切線點：無自共軛直線通過的點稱為 的無切線點，如圖2中的點c。

二級曲線的極點和極線

配極變換 的極點和極線，稱為其對應二級曲線的極點和極線。關於二級曲線的極點與極線有下面結果，

定理1對於二級曲線

直線 的極點方程為

推論1 直線y關於二階曲線(2)'的極點的坐標為

既然曲線的切線就是對應配極的自共軛直線，故它的極點是自共軛點，而自共軛點在曲線上，從而切線就是在曲線上的點的極線，該點就是切點，它是屬於二級曲線的直線的極點。這樣，我們立刻得到

推論2 屬於二級曲線(2)'的任意直線 的切點方程為