基本介紹
- 中文名:超曲面
- 外文名:hypersurface
- 領域:數學
- 適用領域:幾何
超平面




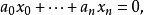

余維數





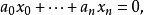


超曲面(英語:hypersurface)是幾何中超平面概念的一種推廣。假設存在一個n維流形M,則M的任一(n-1)維子流形即是一個超曲面。或者可以說,超曲面的余維數為1。...
設M是一個複流形,X是M的真解析子集,若對於每個x∈X,存在U∈Ux和f∈A(U),使得x∩U=f-1(0),則稱x為M的解析超曲面。...
特徵超曲面(characteristic hypersurface)是求解雙曲型方程或研究其解的性質時起重要作用的一種超曲面。...
一般說來,直線與二次曲面相交於兩個點;如果相交於三個點以上,那么此直線全部在曲面上。這時稱此直線為曲面的母線。如果二次曲面被平行平面所截,其截線是二次...
迪潘超曲面(Dupin hypersurface)歐氏空間中的一類特殊超曲面.設M”為R}+‘中的超曲面,若M"的每個主曲率的重數為常數,並且沿著它的主葉層的葉片是常數,則稱M...
內容介紹本書所採用的體裁是運用數理幾何學,以圖解形式來闡述建築造型的百科詞典。本書以圓規、直尺及計算機擅長的多邊形、多面體、曲線、曲面乃至它們的四維徒刑中所...
仿射球面(affine hypersurface)是一個重要的超曲面,指仿射空間中仿射法線交於一點或互相平行非退化的超曲面。一個局部嚴格凸的仿射球稱為虛的或拋物型的仿射球面,...
2.許志才,三維雙曲空間中平行曲面族的兩個定理,《數學雜誌》 1992;3.許志才,常主曲率超曲面的一種幾何刻劃,《東北數學:英文版》 1992 第3期;...
1 水平集 2 超曲面 水平集水平集 編輯 水平集(level set)的基本思想是將界面看成高一維空間中某一函式ψ(稱為水平集函式)的零水平集,同時界面的演化也擴充到...
在具有兩個類的統計分類問題中,決策邊界或決策表面是超曲面,其將基礎向量空間劃分為兩個集合,一個集合。 分類器將決策邊界一側的所有點分類為屬於一個類,而將另...
