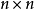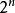格拉斯曼數

在數學物理學中，格拉斯曼數（又稱反交換數）是一種用於狄拉克場路徑積分表示的數學架構。格拉斯曼數是以德國學者赫爾曼·格拉斯曼命名的。

基本介紹

• 中文名：格拉斯曼數
• 別稱：反交換數

性質

各格拉斯曼變數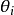 均與代數的實數元無關，它們之間互成反交換關係，但與一般數 間則為交換關係：

。

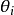
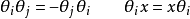
需要注意的是，此算符的平方為零：

由於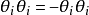 ，所以 。

為了能讓費米子也有路徑積分，格拉斯曼數的積分需要有以下特性：

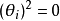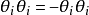
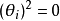
線性

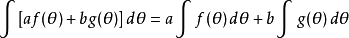
分部積分公式

。

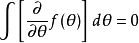
因此格拉斯曼量的積分有以下的規定：

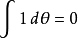
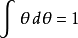
所以結論為任何格拉斯曼數的微分及積分都是相同的。

在量子場論的路徑積分表述中，在描述費米子反交換場時，需要用到以下含格拉斯曼量的高斯積分：

。

其中為矩陣。

由格拉斯曼數集合所生成的代數叫格拉斯曼代數。由個線性獨立的格拉斯曼數生成的代數，其維度為。

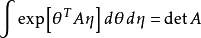
格拉斯曼代數是超交換代數的原型。超交換代數還可以分成偶變數與奇變數，因此可以滿足分層的交換律（特別是奇變數為反交換）。

外代數

格拉斯曼代數是生成元所張成的矢量空間的外代數。外代數的定義與基底的選擇無關。

矩陣表示

格拉斯曼數都能以矩陣形式表示。例如，已知一格拉斯曼代數，是由兩個格拉斯曼數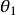及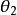所生成。這些格拉斯曼數可用4×4矩陣表示：

。

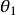
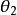
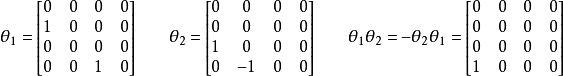
一般來說，由n個生成元生成的格拉斯曼代數，可用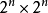的正方形矩陣表示。在物理上，這些矩陣可被視為升算符，作用對象為占位數基底中n個費米子的希爾伯特空間。由於每個費米子的占位數皆為0或1，因此共有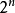種基底態。在數學上，這些矩陣可被視為線性算符，對應與格拉斯曼代數自身的左外乘法。

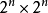
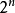
套用

在量子場論中，格拉斯曼數為反交換算符的“經典類比”。它們用於定義費米子場的路徑積分，因此需要為格拉斯曼數的積分下定義，這種積分又叫別列津積分。

格拉斯曼數在為超流形（或超空間）下定義時有重要用途，此時它們被用作“反交換坐標”。