格拉斯曼代數(Grassmann algebra)是各階反變張量空間的並構成的代數,又稱為外代數。
基本介紹
- 中文名:格拉斯曼代數
- 外文名:Grassmann algebra
- 適用範圍:數理科學
簡介
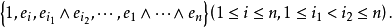
對偶空間
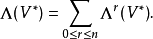
格拉斯曼代數(Grassmann algebra)是各階反變張量空間的並構成的代數,又稱為外代數。
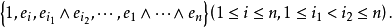
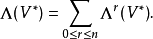
格拉斯曼代數(Grassmann algebra)是各階反變張量空間的並構成的代數,又稱為外代數。...
他建立了格拉斯曼代數和格拉斯曼流形的結構,以及在現代分析和微分幾何中占據重要地位的外微分形式的計算,此外 ,還發展了一種“代數乘法”的運算,從而產生了現在稱為...
在數學物理學中,格拉斯曼數(又稱反交換數)是一種用於狄拉克場路徑積分表示的數學架構。格拉斯曼數是以德國學者赫爾曼·格拉斯曼命名的。...
克利福德代數(Clifford algebra),又稱幾何代數(Geometric algebra),綜合了內積和外...則Λ(V)關於外積成為一個代數,稱為向量空間V的外代數或格拉斯曼代數。...
赫爾曼·甘特·格拉斯曼(Hermann Günther Graßmann,1809年4月15日-1877年9月26日),出生於什切青,是一個博學者,在他生活的時代以語言學家身份聞名,今天以...
他在數學上的主要著作《線性擴張理論》(第 1卷,1844),給出向量外乘法的遞推定義,建立了格拉斯曼代數和格拉斯曼流形的結構,以及在現代分析和微分幾何中占據重要地位...
英國數學家德·摩根和布爾在這方面也做出了重要嘗試。這些工作預示了抽象代數學的產生。另一項引起代數學變革的工作來自英國數學家哈密頓和德國數學家格拉斯曼,前者在...
循環代數(cyclic algebras)是特殊的有限中心單代數。一個有限中心單代數A,若它...引入實域上四元數(1843年)、格拉斯曼(Grassmann,H.G.)引入向量乘法以及凱萊(...
它主要包括近世代數與拓撲、非線性泛函分析、微分流形及其套用、偏微分方程的...3.2.1格拉斯曼代數 3.2.2微分形式 3.2.3外微分 3.2.4龐卡萊引理及逆命題...
幾何代數(Geometric algebra)是以統一模式生成的協變數代數。...... 幾何代數(Geometric algebra)是以統一模式生成的...代數,它有四大基本成分:表示幾何體的格拉斯曼...
代數流形(algebraic manifold)是復射影空間中的代數子集。若P(C)的一個子流...19世紀中葉英國數學家凱萊(1843)、德國數學家格拉斯曼(1844,1861)、瑞士數學家...
代數是數學的一個分支。傳統的代數用有字元 (變數) 的表達式進行算術運算,字元...引入實域上四元數(1843年)、格拉斯曼(Grassmann,H.G.)引入向量乘法以及凱萊(...
克利福德代數是複數、四元數和外代數的推廣。 [1] 二重向量外代數 編輯 外代數(英語:Exterior algebra)也稱為格拉斯曼代數(Grassmann algebra),以紀念赫爾曼·...
Grassmann代數是格拉斯曼在研究線性空間理論時發展出來的代數結構,被費羅貝尼烏斯和達布成功地用於解決普發夫問題。後來E.嘉當系統地發展了外形式和外微分式理論,並且...
多重線性代數研究的內容包括:多重線性映射、具有一定對稱性質的多重線性映射、張量空間、張量對稱類、張量代數、對稱張量代數、格拉斯曼代數、外代數、克利福德代數及其...
