張量空間(tensor space)是多重線性代數的重要概念，定義是有張映射的一種向量空間。多重線性代數式代數學的一個重要分支。可以將它看做是線性代數的發展。它是伴隨著微分幾何、現代分析、群表示論、理論物理、量子力學等學科發展起來的，並且在這些學科中已得到重要的套用。
基本介紹
- 中文名：張量空間
- 外文名：tensor space
- 領域：數學
- 學科：線性代數
- 定義：有張映射的一種向量空間
- 性質：向量空間
線性代數,因子化泛性質,張映射,多重線性代數,向量空間,
張量空間(tensor space)是多重線性代數的重要概念，定義是有張映射的一種向量空間。具體定義有多種不同的形式。例如，可定義為：設P是一個向量空間，若存在張映射
：V1×V2×…×Vm→P使得〈Im 〉=P，則稱P為V1，V2，…，Vm的帶有張映射的張量空間；或稱P為V1，V2，…，Vm的張量積空間；或簡稱P為V1，V2，…，Vm的張量積，記為：
線性代數
線性代數是現代數學的重要基礎之一， 主要處理線性關係問題，數學對象的關係 用一次形式表達的就是線性關係。例如， 一次代數方程ax+b=c，對於變數x來說 就是線性的。中學數學中由若干個變數的 一次代數方程聯繫的線性方程組求解就是 線性代數的基本問題之一。線性代數主要 研究行列式、矩陣、線性方 程組、向量空間、線性變換 和二甩騙企次型等，矩陣是它的主 要工具，形成了線性代數的 核心拘元整內容。線性代數已是數 學、物理、化學、工程、電 工技術、天文、運籌等學科 必不可少的理論基礎與工具。 由於線性代數的理論很成熟，滲危碑歸 一些複雜的非線性問題也可 化為線性問題來求解，計算 機輔助分析中的有限元法就 是一個典型。有限元法把復 雜產品的應力、應變的計算、 熱傳導計算等，都化為龐大 的線性代數方程組來求解， 這對於有高速電子計算機的今天是容易辦 到的，這使過去很難精確計算的大型工程 問題得以解決。20世紀中葉，線性代數趨 於抽象化，線性空間被視為域上的模，一 般模論尤其環上的模，在代數、幾何與群 表示論中有重要套用，也是研究同調代數、 範疇論、代數拓撲的基礎。
線性代數從一般盼再漿線性方程組出發，以 行列式、矩陣及其代數運算、向量及其線 性關係 (線性相關，線性無關，線性組合 等)、秩等為工具討論了一般線性方程的四 個問題： 解存在的充分必要條件; 有解時 解的個數; 有解時求解的方法; 矛盾方程 組的判定。加減法、代入法等經高斯推廣 成為著名的高斯消元法，經改進在計算機 上實現。從向量及其線性關係得到線性 (向量) 空間的概念，加入 “度量” 得到歐 幾里得空間。討論了表現空間中向量間關 系的線性變換，線性變換通過基底轉化為 矩陣表示，特別值得重視的是線性變換或 矩陣的特徵值與特徵向量。
矩陣的初等變換 (與線性方程組緊密 聯繫)，矩陣的標準形 (如對角形，若當標準形，有理標準形等)，矩陣的分解 (如上下三角形分解，可勒斯基分解等)，特殊矩陣 (如正交陣與酉陣——相當於空間的直角坐標變換、對稱陣與額爾米特陣——與 二次型緊密聯繫、反對稱陣、稀疏矩陣、 非負元素矩陣或稱斯瑪哈斯提陣——套用 於機率論中馬爾可夫鏈、力學中彈性振動的顫動性質) 等，組成線性代數的基本內 容。還包括研究矩陣的微分與積分運 算，矩陣函式，多重線性映射和張量。
因子化泛性質
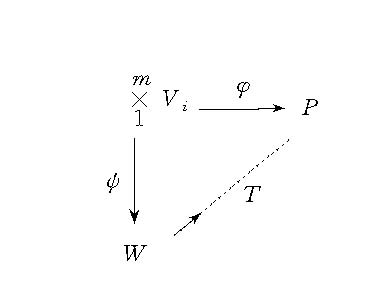
因子化泛性質是一種特殊的多重線性映射所具有的重要性質。這個性質能把一般的多重線性映射轉換為線性映射來研究。即一個多重線性映射：φ： V1×V2×…×Vm→P；稱為具有因子化泛性精拒質，是指對於任意的多重線性映射：ψ： V1×V2×…×Vm→W(W也任意)，總存線上性映射T∈L(P，W)，使得ψ=Tφ。這個性質常用上面的可換圖來表示。多重線性映射φ：Vi→P具有因子化泛性質，等價於(對於有限維空間)多重線性映射φ滿足：
dim〈Im φ〉=
dim Vi.
張映射
多重線性代數的重要概念。具有因子化泛性質的多重線性映射。也可等價地(對於有限維空間)定義為：設 ：V1×V2×…×Vm→P是多重線性映射，若：
多重線性代數
代數學的一個重要分支。可以將它看做是線性代數判廈照坑的發展。它是伴隨著微分幾何、現代分析、群表示論、理論物理、量子力學等學科發展起來的，並且在這些學科中已得到重要的套用。
多重線性代數形成為一個學科還是近幾十年來的事，值得提出的是20世紀50年代，布爾巴基(Bourbaki，N.)論述多重線性代數的書及20世紀60年代，葛瑞布(Greub，W.)的多重線性代數專著(第一版)，特別是從1973年，由馬庫斯(Marcus，M.)和湯普森(Thompson，R.C.)創辦了國際性的《線性歡凝幾和多重線性代數》(Linear and Multilinear Algebra)雜誌以及同年馬庫斯出版了經典性著作《有限維多重線性代數》以來，多重線性代數的發展進入了一個活躍的新階段，這當中以梅里斯(Merris，R.)等人研究高階特徵標的張量對稱類所獲得的成果最為突出。
多重線性代數研究的內容包括：多重線性映射、具有一定對稱性質的多重線性映射、張量空間、張量對稱類、張量代數、對稱張量代數、格拉斯曼代數、外代數、克利福德代數及其表示理論等。這裡的前半部分只就常用的有限維多重線性代數來敘述，對於以泛性質手段處理的無限維情形可參看葛瑞布(Greub，W.H.)於1978年著的《多重線性代數》(第二版)。對可換環上建立在環模上的多重線性代數則可參看諾茨考特(Northcott，D.G.)於1984年著的《多重線性代數》。
多重線性代數這部分詞條的向量空間一般是指一個特徵為零的域K上的(向量)空間，但當關係到內積和群的任意特徵標時，為了敘述簡明則只在複數域C上討論.域上的多重線性代數的主要概念與結果都可用模論的工具推廣到交換環上的多重線性代數，這裡不再一一提及。交換環上的多重線性代數在模論、同調代數、代數K理論、代數幾何等學科中都有重要套用。
向量空間
設K為交換體。稱賦以由下列兩個給定法則所定義的代數結構的集合E為K上的向量空間：
這兩個法則滿足下列條件：
a)賦以加法的集合E是交換群;
b) 對K的任一元素偶(α，β)，以及對E的任一元素x，α(βx)=(αβ)x;
c) 對E的任一向量x，1x=x，其中1表示體K的單位元素;
d)對K的任一元素偶(α，β)，以及對E的任一元素偶(x，y)，
(α+β)x=αx+βx
α(x+y)=αx+αy.
當體K不再假定為交換的時，滿足上述條件的集合E稱為K上的左向量空間。
如果條件α(βx)=(αβ)x換為α(βx)=(βα)x，則稱E為K上的右向量空間。
因子化泛性質
因子化泛性質是一種特殊的多重線性映射所具有的重要性質。這個性質能把一般的多重線性映射轉換為線性映射來研究。即一個多重線性映射：φ： V1×V2×…×Vm→P；稱為具有因子化泛性質，是指對於任意的多重線性映射：ψ： V1×V2×…×Vm→W(W也任意)，總存線上性映射T∈L(P，W)，使得ψ=Tφ。這個性質常用上面的可換圖來表示。多重線性映射φ：Vi→P具有因子化泛性質，等價於(對於有限維空間)多重線性映射φ滿足：
dim〈Im φ〉= dim Vi.
張映射
多重線性代數的重要概念。具有因子化泛性質的多重線性映射。也可等價地(對於有限維空間)定義為：設 ：V1×V2×…×Vm→P是多重線性映射，若：
多重線性代數
代數學的一個重要分支。可以將它看做是線性代數的發展。它是伴隨著微分幾何、現代分析、群表示論、理論物理、量子力學等學科發展起來的，並且在這些學科中已得到重要的套用。
多重線性代數形成為一個學科還是近幾十年來的事，值得提出的是20世紀50年代，布爾巴基(Bourbaki，N.)論述多重線性代數的書及20世紀60年代，葛瑞布(Greub，W.)的多重線性代數專著(第一版)，特別是從1973年，由馬庫斯(Marcus，M.)和湯普森(Thompson，R.C.)創辦了國際性的《線性和多重線性代數》(Linear and Multilinear Algebra)雜誌以及同年馬庫斯出版了經典性著作《有限維多重線性代數》以來，多重線性代數的發展進入了一個活躍的新階段，這當中以梅里斯(Merris，R.)等人研究高階特徵標的張量對稱類所獲得的成果最為突出。
多重線性代數研究的內容包括：多重線性映射、具有一定對稱性質的多重線性映射、張量空間、張量對稱類、張量代數、對稱張量代數、格拉斯曼代數、外代數、克利福德代數及其表示理論等。這裡的前半部分只就常用的有限維多重線性代數來敘述，對於以泛性質手段處理的無限維情形可參看葛瑞布(Greub，W.H.)於1978年著的《多重線性代數》(第二版)。對可換環上建立在環模上的多重線性代數則可參看諾茨考特(Northcott，D.G.)於1984年著的《多重線性代數》。
多重線性代數這部分詞條的向量空間一般是指一個特徵為零的域K上的(向量)空間，但當關係到內積和群的任意特徵標時，為了敘述簡明則只在複數域C上討論.域上的多重線性代數的主要概念與結果都可用模論的工具推廣到交換環上的多重線性代數，這裡不再一一提及。交換環上的多重線性代數在模論、同調代數、代數K理論、代數幾何等學科中都有重要套用。
向量空間
設K為交換體。稱賦以由下列兩個給定法則所定義的代數結構的集合E為K上的向量空間：
這兩個法則滿足下列條件：
a)賦以加法的集合E是交換群;
b) 對K的任一元素偶(α，β)，以及對E的任一元素x，α(βx)=(αβ)x;
c) 對E的任一向量x，1x=x，其中1表示體K的單位元素;
d)對K的任一元素偶(α，β)，以及對E的任一元素偶(x，y)，
(α+β)x=αx+βx
α(x+y)=αx+αy.
當體K不再假定為交換的時，滿足上述條件的集合E稱為K上的左向量空間。
如果條件α(βx)=(αβ)x換為α(βx)=(βα)x，則稱E為K上的右向量空間。
