正交陣是指滿足AA^T=E或者A^T A=E的n階方陣A,其中E為n階單位陣。
基本介紹
- 中文名:正交陣
- 定義:中E為n階單位陣
- 性質:若A是正交陣,則λ=±1
- 充要條件:A行向量或列向量是標準正交向量
定義
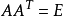
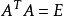
性質
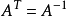

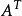
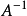

正交陣是指滿足AA^T=E或者A^T A=E的n階方陣A,其中E為n階單位陣。
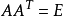
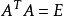
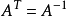

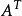
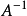
如果AAT=E(E為單位矩陣,AT表示“矩陣A的轉置矩陣”)或ATA=E,則n階實矩陣A稱為正交矩陣。正交矩陣是實數特殊化的酉矩陣,因此總是屬於正規矩陣。儘管我們在這裡...
正交陣是指滿足AA^T=E或者A^T A=E的n階方陣A,其中E為n階單位陣。...... 正交陣是指滿足AA^T=E或者A^T A=E的n階方陣A,其中E為n階單位陣。...
正交是線性代數的概念,是垂直這一直觀概念的推廣。而正交關係往往是指向量之間或者矩陣執之間的關係。...
“正交性”是從幾何中借來的術語。如果兩條直線相交成直角,他們就是正交的。用向量術語來說,這兩條直線互不依賴。沿著某一條直線移動,該直線投影到另一條直線上...
線上性代數中,正交變換是線性變換的一種,它從實內積空間V映射到V自身,且保證變換前後內積不變。因為向量的模長與夾角都是用內積定義的,所以正交變換前後一對向量...
正交表示是正交變換的推廣。有限群在實數域上的任意的矩陣表示都等價於一個正交表示。...
正交編碼是一種典型通信編碼技術,具有良好的抗噪性能,能有效消除脈衝邊緣振盪造成的干擾,在通信編碼時能有效提高準確性。...
1925年,科學名詞審查會算學名詞審查組在《科學》第十卷第四期刊登的審定名詞表中,矩陣被翻譯為“矩陣式”,方塊矩陣翻譯為“方陣式”,而各類矩陣如“正交矩陣”...
旋轉矩陣不包括點反演,點反演可以改變手性,也就是把右手坐標系改變成左手坐標系或反之。所有旋轉加上反演形成了正交矩陣的集合。旋轉可分為主動旋轉與被動旋轉。...
都等於0。一個投影是正交投影,若且唯若它是自伴隨的變換,這意味著正交投影的矩陣有特殊的性質。如果投影是在實向量空間中,那么它對應的矩陣是對稱矩陣: 。如果投...
Hn為正交方陣,所謂正交矩陣指它的任意兩行(或兩列)都是正交的。並且行列式為 。性質2:任意一行(列)的所有元素的平方和等於方陣的階數。即:設A為n階由+1和-...
正交線性替換:如果線性替換 X=CY 的矩陣C是正交矩陣,則稱之為正交線性替換。 如果A為n階實矩陣,A稱為正交矩陣,如果:A×A′=E。 ...
么正矩陣表示的就是厄米共軛矩陣等於逆矩陣。對於實矩陣,厄米共軛就是轉置,所以實正交表示就是轉置矩陣等於逆矩陣。實正交表示是么正表示的特例。...
舒爾正交關係(Schur orthogonality relations)描述了有限群表示中的核心事實。它可以推廣到一般的緊群,特別是緊李群,比如旋轉群 SO(3)。此關係可藉由舒爾引理證明。...
現在,正交性是一種數學屬性,產生於描述系統質量和剛度矩陣的特徵解。特徵解的一個副產物是,矢量“線性獨立”,矢量“關於質量和剛度矩陣同時正交”。所以正交性是一...
我們把這3個正交的單位向量稱為空間坐標系的基,它們單位長度為1且正交,所以可以成為標準正交基。三個向量叫做基向量。現在我們用矩陣形式寫出基向量和基。i...
線上性代數中用矩陣(向量)代替代數式中的實數,得到的代數式稱為矩陣代數式。...定理 實對稱矩陣的正交相似性任意一個實對稱矩陣,一定相似正交與一個實對角矩陣...
2.1 對稱矩陣、Hermitian 矩陣與循環矩陣2.2 基本矩陣2.3 置換矩陣、互換矩陣與選擇矩陣2.4 正交矩陣與酉矩陣2.5 帶型矩陣與三角矩陣...
數學上,任一的MxN離散線性轉換皆可表示成矩陣(Matrix) 的型式:Y=AX,再進一步假設,若矩陣Aby正交基底 (Orthogonal basis) 列向量(Row vector) 所組成,也可表示...
在矩陣論的發展史上,弗羅伯紐斯(G.Frobenius,1849-1917)的貢獻是不可磨滅的。他討論了最小多項式問題,引進了矩陣的秩、不變因子和初等因子、正交矩陣、矩陣的相似...
