線性方程組是各個方程關於未知量均為一次的方程組(例如2元1次方程組)。對線性方程組的研究,中國比歐洲至少早1500年,記載在公元初《九章算術》方程章中。
線性方程組有廣泛套用,熟知的線性規劃問題即討論對解有一定約束條件的線性方程組問題。
基本介紹
簡介
定義
解法
 ⑴
⑴ 線性方程組
線性方程組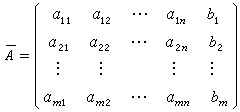 線性方程組
線性方程組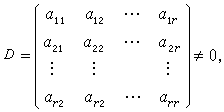 線性方程組
線性方程組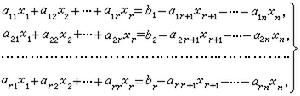 ⑵
⑵ 線性方程組
線性方程組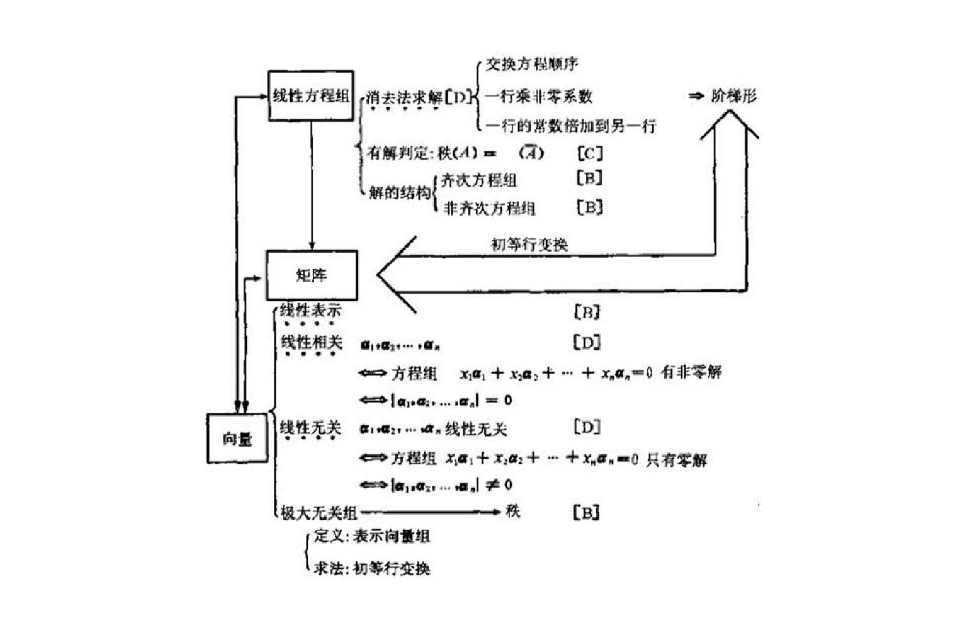
線性方程組是各個方程關於未知量均為一次的方程組(例如2元1次方程組)。對線性方程組的研究,中國比歐洲至少早1500年,記載在公元初《九章算術》方程章中。
線性方程組有廣泛套用,熟知的線性規劃問題即討論對解有一定約束條件的線性方程組問題。
 ⑴
⑴ 線性方程組
線性方程組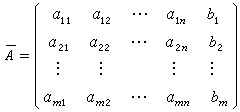 線性方程組
線性方程組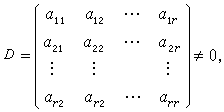 線性方程組
線性方程組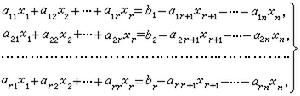 ⑵
⑵ 線性方程組
線性方程組線性方程組是各個方程關於未知量均為一次的方程組(例如2元1次方程組)。對線性方程組的研究,中國比歐洲至少早1500年,記載在公元初《九章算術》方程章中。線性方程...
齊次線性方程組:常數項全部為零的線性方程組。如果m<n(行數小於列數,即未知數的數量大於所給方程組數),則齊次線性方程組有非零解,否則為全零解。...
二元線性方程組,別名叫“二元一次方程組”,是指由兩個方程兩個未知量構成的線性方程組。二元線性方程組實質上就是二元一次方程組。因為二元一次方程的圖象是一條...
常數項不全為零的線性方程組。...... 非齊次線性方程組定義 編輯 常數項不全為零的線性方程組稱為非齊次線性方程組。非齊次線性方程組的表達式為:Ax=b...
線性微分方程組(first order linear differentialequation system)是由幾個微分方程聯立起來共同確定幾個具有同一自變數的函式的情形.這些聯立的微分方程稱為微分方程組...
完全三角形方程組是一種特殊的線性方程組。係數矩陣是對角元素全不為零的上(下)三角方陣的線性方程組叫做完全上(下)三角形方程組,簡稱完全三角形方程組。完全三角...
由實際問題得到的方程組的係數矩陣或者常數向量的元素,本身會存在一定的誤差;這些初始數據的誤差在計算過程中就會向前傳播,從而影響到方程組的解。病態方程組是指因...
三元齊次線性方程組(system of ternary homogeneous linear equations)亦稱三元一次齊次方程組,是一種特殊的線性方程組,即方程組中的各個方程的常數項都是零的三元...
形如y'+P(x)y=Q(x)的微分方程稱為一階線性微分方程,Q(x)稱為自由項。一階,指的是方程中關於Y的導數是一階導數。線性,指的是方程簡化後的每一項關於y...
代數方程組(system of algebraic equations)是由多個n元多項式方程所構成的方程組,由數域P上m個n元多項式fi(x1,x2,…,xn)(i=1,2,…,m)組成的方程組稱為...
超定方程組是指方程個數大於未知量個數的方程組。對於方程組Ra=y,R為n×m矩陣,如果R列滿秩,且n>m。則方程組沒有精確解,此時稱方程組為超定方程組。...
相容方程是一個數學用語,若線性方程組AX=B有解, 則稱AX=B為相容方程組,也可以稱為線性方程組AX=B相容。若其無解則稱為不相容。...
矛盾方程組(contradictory equations)是一種特殊的方程組,在求解範圍內無解(解集為空集)的方程組稱為這個範圍內的矛盾方程組。一個方程組中,若有一個矛盾方程,...
矛盾線性方程組(over-determined linear sys-tem)亦稱超定線性方程組一類特殊的代數方程 組.指方程個數多於未知量個數時的線性代數方程組.這類問題在實踐中經常...
大型稀疏矩陣線性化方程組的數值求解問題 廣泛存在於工程實踐尤其是計算機仿真領域 如水力管網計算,電力系統的大型導納矩陣計算,高階偏微分方程的數值求解,以及鑄件充...
非線性方程,就是因變數與自變數之間的關係不是線性的關係,這類方程很多,例如平方關係、對數關係、指數關係、三角函式關係等等。求解此類方程往往很難得到精確解,經常...
解矛盾線性方程組的最小二乘法(least squaremethod solving over-determined linear system)最小二乘法的一種.指採用最小二乘準則求解矛盾線性方程組的一個常用...
計算矩陣的秩的一個有用套用是計算線性方程組解的數目。如果係數矩陣的秩等於增廣矩陣的秩,則方程組有解。在這種情況下,如果它的秩等於方程(未知數)的數目,則...
線性代數是數學的一個分支,它的研究對象是向量,向量空間(或稱線性空間),線性變換和有限維的線性方程組。向量空間是現代數學的一個重要課題;因而,線性代數被廣泛地...
齊次線性方程組的解集的極大線性無關組稱為該齊次線性方程組的基礎解系。基礎解系是線性無關的,簡單的理解就是能夠用它的線性組合表示出該方程組的任意一組解,...
克萊姆法則,又譯克拉默法則(Cramer's Rule)是線性代數中一個關於求解線性方程組的定理。它適用於變數和方程數目相等的線性方程組,是瑞士數學家克萊姆(1704-1752)...
二階行列式指4個數組成的符號,其概念起源於解線性方程組,是從二元與三元線性方程組的解的公式引出來的,因此我們首先討論解方程組的問題。行列式是一個重要的數學...
數學上,高斯消元法(或譯:高斯消去法),是線性代數規劃中的一個算法,可用來為線性方程組求解。但其算法十分複雜,不常用於加減消元法,求出矩陣的秩,以及求出...
增廣矩陣(又稱擴增矩陣)就是在係數矩陣的右邊添上一列,這一列是線性方程組的等號右邊的值。...
初等變換(elementary transformation)是三種基本的變換,出現在《高等代數》中。初等變換包括:線性方程組的初等變換、行列式的初等變換和矩陣的初等變換,這三者在本質上...
