基本介紹
- 中文名:矛盾方程組
- 外文名:contradictory equations
- 所屬學科:數學
- 所屬問題:初等代數(方程)
- 相關概念:對稱矩陣,矩陣的秩,正定矩陣等
矛盾方程組及其求解




相關概念及定理











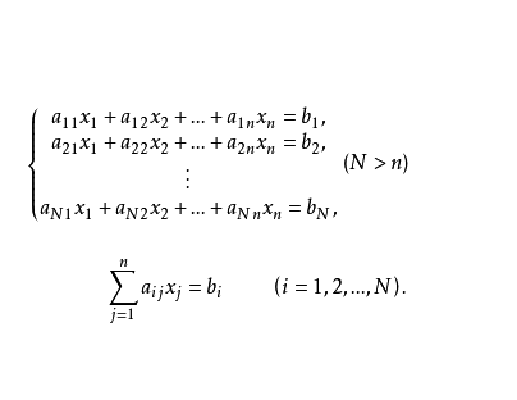















矛盾方程組(contradictory equations)是一種特殊的方程組,在求解範圍內無解(解集為空集)的方程組稱為這個範圍內的矛盾方程組。一個方程組中,若有一個矛盾方程,...
矛盾線性方程組(over-determined linear sys-tem)亦稱超定線性方程組一類特殊的代數方程 組.指方程個數多於未知量個數時的線性代數方程組.這類問題在實踐中經常...
矛盾方程(contradictory equation)亦稱矛盾等式,是一種特殊方程,即無解的方程。它有以下兩種形式:1.數值矛盾方程的意義是:在求解範圍內沒有解(或說解集是空集)的...
解矛盾線性方程組的最小二乘法(least squaremethod solving over-determined linear system)最小二乘法的一種.指採用最小二乘準則求解矛盾線性方程組的一個常用...
超定方程組是指方程個數大於未知量個數的方程組。對於方程組Ra=y,R為n×m矩陣,如果R列滿秩,且n>m。則方程組沒有精確解,此時稱方程組為超定方程組。...
解方程:求出方程的解的過程,也可以說是求方程中未知數的值的過程,或說明方程無解的過程叫解方程。方程中,恆等式叫做恆等方程,矛盾式叫做矛盾方程。在未知數等於...
能夠使方程左右兩邊的值相等的未知數的值,叫做方程的解。多元方程的解是一組...無解的方程叫做矛盾方程,故矛盾方程的解集是空集 [2] 。求出方程的所有的解...
(方程的個數大於未知量的個數),這個方程系統稱為矛盾方程組(Over Determined System),如果 (方程的個數小於未知量的個數),這個系統就是Under Determined System。...
(線性相關,線性無關,線性組合 等)、秩等為工具討論了一般線性方程的四個問題: 解存在的充分必要條件; 有解時 解的個數; 有解時求解的方法;矛盾方程組的判定...
6.5 矛盾方程組的極小最小二乘解與廣義逆矩陣A+ 1876.5.1 矛盾方程組的極小最小二乘解 1876.5.2 廣義逆矩陣A+的常用性質 191...
6.2.2相容方程組的通解與A-2746.2.3相容方程組的極小範數解與A-m2776.2.4矛盾方程組的最小二乘解與A-l2816.2.5線性方程組的極小最小二乘解與A+...
7.2.4 矛盾方程組的極小範數最小二乘解與A+ 7.3 矩陣的直積及其套用 7.3.1 直積的概念 7.3.2 直積的性質 7.3.3 線性矩陣方程的可解性 習題7 習...
三次樣條插值122 習題五132 第六章 最小二乘法與曲線擬合1356.1 用最小二乘法求解矛盾方程組1356.2 多項式擬合141 習題六148 第七章 數值積分與數值微分150...
5.2 相容方程組的極小範數解和廣義逆Am-5.3 矛盾方程組的最小二乘 解和廣義逆Ai-5.4 線性方程組的極小最小二乘和廣義逆A+...
習題與註解第2章 線性代數方程組的直接解法2.1 簡單情形2.2 Gauss消去法2.3 三角分解2.4 正交三角分解法2.5 線性矛盾方程組的最小二乘法...
6.2.4矛盾方程組的最小二乘解與A-l312 6.2.5線性方程組的極小最小二乘解與A+317 習題6318 第7章幾類特殊矩陣與特殊積323 引言什麼是特殊矩陣與特殊積323...
3.3 解矛盾方程組3.4 程式示例習題3第4章 非線性方程求根4.1 實根的對分法4.2 疊代法4.3 牛頓疊代法4.4 弦截法4.5 非線性方程組的牛頓方法4.6 程式示例...
*4.6廣義逆矩陣與線性方程組的求解4.6.1A(1)與線性方程組的解4.6.2A(1,4)與線性方程組的極小範數解4.6.3A(1,3)與矛盾方程組的最小二乘解...
第一節 用最小二乘法解矛盾方程組 第二節 多項式擬合 第三節 C語言實現的算法 一、 用單精度求方程組的個數比未知 數多的聯立一次方程組的解(一) ...
