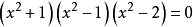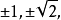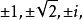一元方程

一元方程(monadic equation)是一種最簡單的方程，指含有一個未知數的方程，更確切的意義是：如果一個方程中，有若干個字母，當把其中某一個字母當成未知數，而把其餘字母當成已知數時，方程就稱為該字母的一元方程。在討論多元方程時，也可以出現除一個元外，含有其他各元的項的係數均為零而成為一元方程的情形。例如x+1=0可看成x，y的二元方程x+0y+1=0，它在平面直角坐標系中表示一條直線。

基本介紹

• 中文名：一元方程
• 外文名：monadic equation
• 所屬學科：數學
• 所屬問題：代數與初等函式
• 簡介：含有一個未知數的方程

基本介紹

在數域F上只含有一個未知數的方程，叫做F上的一元方程，一元一次方程、一元二次方程等都是一元方程。一元方程的解又叫做方程的根。

含有未知數的等式叫做關於這個(或這些)未知數的方程，簡稱方程。方程中的未知數叫做方程的元。含有幾個未知數的方程就叫做幾元方程。例如，關於x的方程ax=b，就是以x為未知數的一元方程。等式F₁(x，y，z)=F₂(x，y，z)就表示一個以x，y，z為元的三元方程。

一元方程的解與解集

能夠使方程左右兩邊的值相等的未知數的值，叫做方程的解。多元方程的解是一組未知數的值。如x=2，y=1是二元方程2x-y=3的一個解。

一元方程的解也叫做方程的根。如果一個方程的全體根中有幾個根相等，那么這幾個根叫做重根。例如一元方程x³(x-1)²(x+3)=0，它的根是x₁=x₂=x₃=0，x₄=x₅=1，x₆=-3，那么“0”就是它的三重根，“1”就是它的二重根，“-3”不是重根，可以稱之為單根，一般只對整式方程研究重根問題。

一個方程的解的全體所組成的集合，叫做這個方程的解的集合，簡稱解集。若方程無解，解集就是空集。無解的方程叫做矛盾方程，故矛盾方程的解集是空集。

求出方程的所有的解或判斷方程無解的過程，叫做解方程。在不同的數集裡解同一個方程，所得的解集不一定相同。例如一元方程

在有理數集裡有兩個根是±1，其解集是{1，-1};在實數集裡有四個根是

那么在實數集裡解此方程所得解集為

在複數集裡解此方程則有六個根：

故得解集為

再如方程

在實數集裡是矛盾方程，在複數集裡則不是矛盾方程。一般地，應指明在什麼範圍(數域)里研究。中學數學裡解方程時若不明確求解的範圍(數域)，即是指在實數域裡求解。