基本介紹
- 中文名:一元六次方程
- 係數:a b c d e f
- 常數:g
- 條件:a,b,c,d,e,f,g∈R,且a≠0
- 阿貝爾定理:不存在一般五次方程求根公式
- 可否解:普遍不可
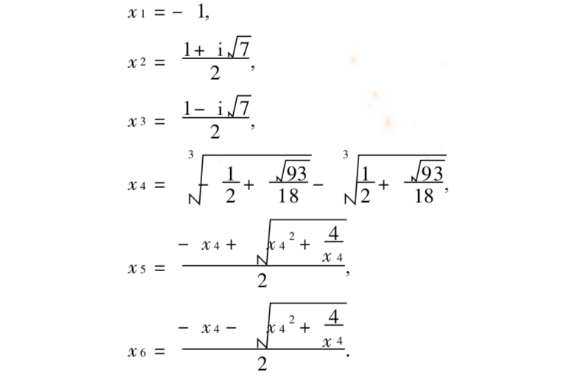
16 世紀時,義大利數學家塔塔利亞和卡當等人,發現了一元三次方程的求根公式,費拉里找到了四次方程的求根公式。當時數學家們非常樂觀,以為馬上就可以寫出五次方程、六...
在代數中,一個多項式是一個六項式的多項式。六次方程式或六元方程式是六度多項式方程式,即左手側是一個多項式並且右側為零的方程式。...
求一元五次方程的根式解曾困擾數學家三百餘年,阿貝爾和伽羅瓦的工作證明了一般一元五次方程沒有根式解。1930 年華羅庚《蘇家駒之代數的五次方程式解法不能 成立之...
一元n次方程(equation of degree n with one unknown)是一元n次多項式所確定的方程,指方程a0xn+a1xn-1+…+an=0 (a0≠0),當n≥3時,稱為高次方程.研究...
一元八次方程指根據阿貝爾定理,≥5次的方程無根式解,而對於些特殊的方程來說,一定有根式解。注:當前的求根公式沒有經過嚴格的數論推導,僅在特殊的八次方程中...
只含有一個未知數(即“元”),並且未知數的最高次數為3(即“次”)的整式方程叫做一元三次方程(英文名:cubic equation in one unknown)。一元三次方程的標準...
其中:a,b,c,d,e,f,g,h,j,k,l被稱為方程的係數(零次項係數也稱為...其中:xn(n=1,2,3,4,5,6,7,8,9,10)被稱為該一元十次方程的十個根。...
其中:xn(n=1,2,3,4,5,6,7,8)被稱為該一元八次方程的八個根。一元八次方程求根公式根與係數的關係 編輯 一元八次方程求根公式完整公式 編輯 ...
只含有一個未知數(一元),並且未知數項的最高次數是2(二次)的整式方程叫做一元二次方程。一元二次方程經過整理都可化成一般形式ax²+bx+c=0(a≠0)。...
標準型的一元三次方程aX^3+bX^2+cX+d=0(a,b,c,d∈R,且a≠0),其解法有:1、義大利學者卡爾丹於1545年發表的卡爾丹公式法;2、中國學者范盛金於1989年發表...
只含有一個未知數(即“元”),並且未知數的最高次數為5(即“次”)的整式方程叫做一元五次方程(英文名:Quintic Equation)。一元五次方程的標準形式(即所有一元...
一元方程(monadic equation)是一種最簡單的方程,指含有一個未知數的方程,更確切的意義是:如果一個方程中,有若干個字母,當把其中某一個字母當成未知數,而把其餘...
人類很早就掌握了一元二次方程的解法,但是對一元三次方程的研究,則是進展緩慢。古代中國、希臘和印度等地的數學家,都曾努力研究過一元三次方程,但是他們所發明...
二元二次方程的套用 一個未知數的代數式表示另一個未知數,然後代入二元二次方程中,從而化“二元”為“一元”,如此便得到一個一元二次方程。此時,方程組解的情...
完全一元二次方程是一類簡單的代數方程,即具有標準形式且一次項係數與常數項均不為零的一元二次方程。當一次項係數與常數項至少有一個為零時則稱為不完全一元...
