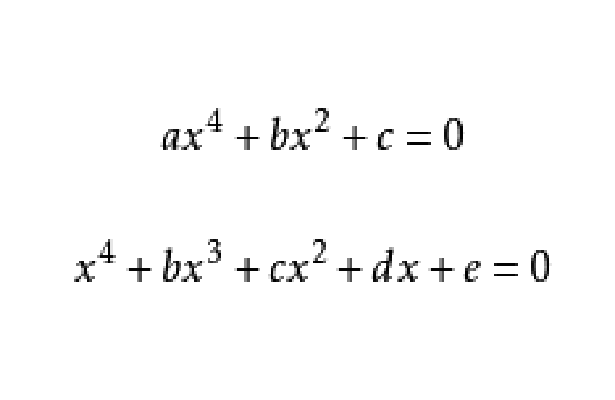四次方程

四次方程是未知數最高次數為四次的多項式方程。本篇只討論一元四次方程，並簡稱為四次方程。

基本介紹

• 中文名：四次方程
• 外文名：Quartic equation
• 所屬類別：多項式方程
• 所屬領域：數理科學
• 著名人物：費拉里、卡丹、歐拉等
• 相關著作：卡丹的《重要的藝術》

基本介紹

四次方程屬於高次方程範疇，其基本解法思想是：通過適當的配方，使四次方程變為兩個一元二次方程．

一元四次方程的求解，據說是由卡爾達諾的學生費拉里(Ferrari，1522年2月2日到1565年10月5日)首先掌握的．費拉里曾利用它戰勝了塔爾塔利亞．

四次方程的求解主要是以下兩種情況：

1.如果一個一元四次方程的三次項係數和一次項係數都為 ，那么該一元四次方程是雙二次方程：

2.一般的一元四次方程可化為：

這種一般情況主要有兩種解決方法：（1）Euler(歐拉)；（2）Ferrari(費拉里)，此處詳細陳述第二種。

解法

特殊情況

如果一個一元四次方程的三次項係數和一次項係數都為0 ，那么該一元四次方程是雙二次方程：

令 ，得 。用一元二次方程的求根公式可求出

則原方程的四個根分別為：

一般情況

1

一般的一元四次方程可化為：

Ferrari(費拉里)

移項可得：

兩邊同時加上 配成平方：

在兩邊同時加上 ，可得：

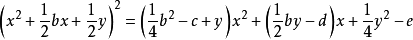
若使右邊這個x的二次式的判別式等於零，就能使這一邊成為x的一次式的完全平方。於是設

這是y的一個三次方程。選取這三次方程的任一個根代入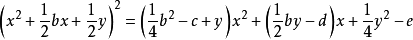

中的y。根據左邊

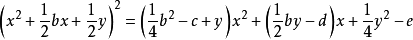
也是個完全平方這一事實，取平方根，得到x的一個二次式，它等於x的兩個互為正負的線性函式之一。解出這兩個二次方程便得到x的4個根。若從

選取另一個根就會從

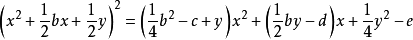
引出一個不同的方程但得到同樣的四個根。

費拉里發現的上述解法的創造性及巧妙之處在於：

第一次配方後引進參數 y，並再次配方把左邊配成含有參數 y 的完全平方，再使 右邊也成為完全平方，從而把一個一元四次方程的求解問題化成了一個一元三次方程及兩個一元二次方程的求解問題．

因此，我們可得四次方程求根公式。

2