簡介,貢獻,作者簡介,相關資料,卷首,梯法七乘方圖,四元自乘演段圖,假令四草,卷上,直段求源,混積問元,端匹互隱,廩粟回求,商功修築,和分索隱,卷中,如意混和,方圓交錯,三率究圓,明積演段,勾股測望,或問歌彖,茭草形段,箭積交參,拔換截田,五問。,卷下,果垛疊藏,鎖套吞容,方程正負,雜范類會,兩儀合轍,左右逢元,三才變通,四象朝元,版本,
簡介
它是一部成就輝煌的
數學名著,受到近代
數學史研究者的高度評價,認為是中國數學著作中最重要的一部,同時也是
中世紀最傑出的數學著作之一。但其美中不足的是,在四元玉鑒中,對於一些重要的問題如求解高次聯立方程組的消去法等解說過於簡略,並且對於書中每一個問題的解法也沒有列出詳細的演算過程,故比較深奧,人們很難讀懂。以致於自朱世傑之後,中國這種在數學上高度發展的局面不但沒有保持發展下去,反而很多成就在明、清的一段時期內幾乎失傳。
此外朱世傑將高階等差級數求和和高次內插法進行了發展。《四元玉鑒》是元代傑出數學家朱世傑的代表作,其中的成果被視為中國籌算系統發展的頂峰。
貢獻
《四元玉鑒》是朱世傑闡述多年研究成果的一部力著。全書共分3卷,24門,288問,書中所有問題都與求解方程或求解方程組有關,其中四元的問題(需設立四個未知數者)有7問,三元者13問,二元者36問,一元者232問。卷首列出了賈憲三角等四種五幅圖,給出了天元術、二元術、三元術、四元術的解法範例;後三者分別是二元、三元、四元高次方程組的列法及解法。創造四元消法,解決多元高次方程組問題是該書的最大貢獻,書中另一個重大成就是系統解決高階等差級數求和問題和高次招差法問題。
在朱世傑之前,古代中國數學已有了解方程的方法———“天元術”,“天元術”解方程是設“天元為某某”,某某就是(x)。朱世傑不僅繼承沿用了天元術,方程組解法由二元、三元推廣至四元。未知數不止一個時,除設未知數天元(x)外,還設地元(y)、人元(z)及物元(u),再列出二元、三元甚至四元的高次聯立方程組,然後求解。在
歐洲,解聯立一次方程始於16世紀,關於多元高次聯立方程的研究則是18、19世紀的事了,朱世傑的“天元術”比歐洲早了400多年。
朱世傑對“垛積術”的研究,實際上得到了高階等差級數求和問題的普遍的解法。自宋代起我國就有了關於高階等差級數求和問題的研究,
沈括(1031-1095年)和楊輝(1261-1275年)的著作中,都有垛積問題,這些垛積問題有一些就涉及高階等差級數,朱世傑在《四元玉鑒》中又把這一問題的研究進一步深化,得到了一串三角垛的公式。
《四元玉鑒》是一部成就輝煌的數學名著,是宋元數學集大成者,也是我國
古代水平最高的一部數學著作。現代數學史研究者對《四元玉鑒》給予了高度評價。著名科學史專家
喬治·薩頓說,《四元玉鑒》“是中國數學著作中最重要的一部,同時也是中世紀最傑出的數學著作之一”。編著《
中國科學技術史》的
李約瑟這樣評價朱世傑和《四元玉鑒》:“他以前的數學家都未能達到這部精深的著作中所包含的奧妙的道理”。
朱世傑之後,元代再無高深的數學著作出現,漢唐宋元的數學著作很少有新的刻本,很多甚至失傳了。乾隆三十七年(1772年)開《
四庫全書》館時,挖掘了不少古代數學典籍,朱世傑的著作卻未被發現,因此,起初沒有編入;1799年
阮元、
李銳等人編纂數學家傳記《疇人傳》時,也未介紹《四元玉鑒》。之後不久,阮元在
浙江訪得此書,旋即將其編入《四庫全書》,並把抄本交給李銳校算(未校完),後由何元錫按此抄本刻印,這是《四元玉鑒》1303年初版以來的第一個重刻本。1839年
揚州學者羅士琳經多年研究之後,出版了他所編著的《四元玉鑒細草》,羅氏對《四元玉鑒》書中每一問題都作了細草。就在羅士琳翻刻《四元玉鑒》時,《算學啟蒙》也還無著落。後來羅士琳“聞
朝鮮以是書為算科取士”,於是請
人在北京找到了順治十七年(1660年)朝鮮
全州府尹金始振所刻的翻刻本,這樣,《算學啟蒙》又在揚州重新刊印出版,這就是該書現存各種版本的母本。
元代朱世傑這兩部傑出的數學著作都是在揚州完成、刻印的,失傳了幾百年後,它們又被揚州學者發現、校算、注釋,並在揚州重新刻印出版,僅此可見,揚州在我國數學發展史上有著十分重要的地位。
作者簡介
朱世傑(1249年-1314年),字漢卿,號松庭,
漢族,
燕山(今
北京)人氏,元代數學家、
教育家,畢生從事數學教育。朱世傑在當時天元術的基礎上發展出“四元術”,也就是列出四元高次多項式方程,以及消元求解的方法。此外他還創造出“垛積法”,即
高階等差數列的求和方法,與“招差術”,即高次內插法。主要著作是《
算學啟蒙》與《四元玉鑒》。
朱世傑“以數學名家週遊湖海二十餘年”,“踵門而學者雲集”(莫若、祖頤:《四元玉鑒》後序)。朱世傑數學代表作有《算學啟蒙》(1299)和《四元玉鑒》(1303)。
《算學啟蒙》是一部通俗
數學名著,曾流傳海外,影響了朝鮮、
日本數學的發展。《四元玉鑒》則是中國宋元數學高峰的又一個
標誌,其中最傑出的數學創造有“四元術”(多元高次方程列式與消元解法)、“垛積術”(高階等差數列求和)與“
招差術”(高次內插法)。
宋元時期,中國數學鼎盛時期中傑出的數學家有“秦﹝九韶﹞、李﹝冶﹞、楊﹝輝﹞、朱﹝世傑﹞四大家”,朱世傑就是其中之一。朱世傑是一位平民數學家和數學教育家。朱世傑平生勤力研習《
九章算術》,旁通其它各種算法,成為元代著名數學家。
相關資料
在元滅南宋以前,南北之間的交往,特別是學術上的交往幾乎是斷絕的。南方的數學家對北方的天元術毫無所知,而北方的數學家也很少受到南方的影響。朱世傑曾“週遊四方”,莫若(古代數學家)序中有“燕山松庭
朱先生以數學名家週遊湖海二十餘年矣。四方之來學者日眾,先生遂發明《九章》之妙,以淑後圖學,為書三卷……名曰《四元玉鑒》”,祖頤後序中亦有“漢卿名世傑,松庭其自號也。周流四方,復游
廣陵,踵門而學者雲集”。經過長期的遊學、講學等活動,終於在1299年和1303年,在揚州,刊刻了他的兩部數學傑作——《算學啟蒙》和《四元玉鑒》。楊輝書中的歸除歌訣在朱世傑所著《算學啟蒙》中有了進一步的發展。
 《四元玉鑒》
《四元玉鑒》清
羅士琳認為:“漢卿在宋元間,與秦道古(即
秦九韶)、李仁卿可稱鼎足而三。道古正負開方,漢卿天元如積皆足上下千古,漢卿又兼包眾有,充類儘量,神而明之,尤超越乎秦、李之上”。清代數學家
王鑑也說:“朱松庭先生兼秦、李之所長,成一家之著作”。朱世傑全面繼承了並創造性地發揚了天元術、正負開方法等秦、李書中所載的數學成就之外,還囊括了
楊輝書中的日用、商用、歸除歌訣之類與當時社會生活密切相關的各種算法,並作了新的發展。
由此看來,在朱世傑的工作中,不僅有高次方程的解法,天元術等為代表的北方數學的成就,也包括了楊輝工作中所體現出來的日用,商用算法以及各種歌訣等南方數學的成就,不僅繼承了古代中國數學的光輝遺產,而且又作了創作性的發展。朱世傑的工作,在一定意義上講,可以看作是宋元數學的代表,可以看作是古代籌算系統發展的頂峰。就連西方資產階級學者們也不能否認這一點,喬治·薩頓說:朱世傑“是中國的,他所生存的時代的,同時也是貫穿古今的一位最傑出的數學家”,說《四元玉鑒》“是中國數學著作中最重要的一部,同時也是中世紀最傑出的數學著作之一”。朱世傑以他自己的傑出著作,把中國古代數學推向更高的境界,為中國古代數學的光輝史冊,增加了新的篇章,形成了宋代中國數學發展的最高峰。
卷首
卷首是全書的預備知識。
梯法七乘方圖
 朱世傑《四元玉鑒》卷首的「古法七乘方圖」
朱世傑《四元玉鑒》卷首的「古法七乘方圖」這是賈憲三角形的推廣
四元自乘演段圖
朱世傑給出
的幾何圖(演段圖)
 四元自乘演段圖
四元自乘演段圖下圖為四元自乘演段圖的現代形式:
 四元自乘演段圖
四元自乘演段圖立四元
中見為“太”,上為x,下為z,左為y,右為w:
 立四元
立四元四元自乘
 四元的自乘
四元的自乘假令四草
包括一氣混元、兩儀化元、三才運元、四象會元,代表一、二、三、四次方程。
一氣混元
本節闡明天元術。
今有黃方乘直積得二十四步,只雲股弦和九步,問勾幾何?
答曰:三步。
草曰:立天元一為勾
根據條件 黃方乘直積得二十四步
:此外:股弦和九步
 一氣混元
一氣混元
由此得方程
解之,得勾=3
兩儀化元
本節闡明二元術。
今有股冪減弦較較與股乘勾等。只雲勾冪加弦較和與勾乘弦同。問股幾何?
答曰:四步 草曰:立天元一為股,地元一為勾弦和。天地配合求解得方程:
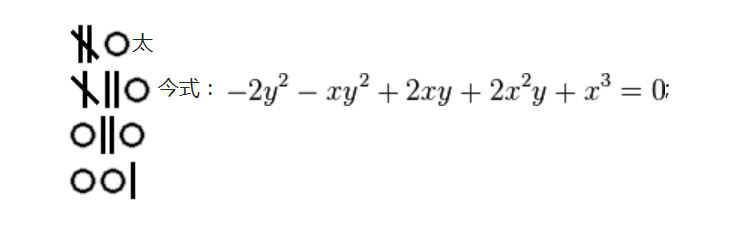 兩儀化元
兩儀化元又根據所給條件得:
 雲式
雲式由此得:
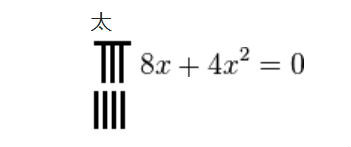 8x+4xx=0
8x+4xx=0和

 2x平方+x3方
2x平方+x3方相消得
 x=4
x=4解之,得
三才運元
本節闡明三元術
朱世傑在《三才運元》一節,比較詳細的闡述逐次消元法,受到國內外學者的重視
今有股弦較除弦和與直積等。只雲勾股較除弦較和與勾同。問弦幾何?
得到
雲式:
三元式
三元式與雲式相消,
人天易位 人弦-->天勾
得:
前式
後式
相消得
 三儀化圓
三儀化圓解之得 x=5,即 天勾=5;
人天易位 天勾-->人弦
得弦=五步。
四象會元
本節闡明四元術。
 四象會元
四象會元今有股乘五較與弦冪加勾乘弦等。只雲勾除五和與股冪減勾弦同。問黃方帶勾股弦共幾何?''
:答曰:一十四{{0}} 步。
:草曰:立天元{{0}} 一為勾,地元一為股,人元一為弦,物元一為開數。
得四元方程
消元,物易天位
 物易天位
物易天位解之,
物易天位,得 十四步。
卷上
混積問元
直段求源
一十八問。第十八問:
今有積以和乘之,減積,余以平乘之加和,得一十七萬一百六十二步。只雲和為益實。四為益方,三為從上廉,二為益下廉,一為正隅,三平方開之,如平四分之一。問,長,平各幾何?
答曰:平一十二步,長三十步。
立天元一為開方數,得十次方程:
解之得 x=3, 乘四得12, 即平數。
混積問元
十八問
端匹互隱
九問
廩粟回求
六問
商功修築
七問
和分索隱
一十三問。
卷中
 今有圓城
今有圓城如意混和
二問
方圓交錯
九問
三率究圓
一十四問
|今有平圓積四十九步三百一十四分步之二百三十九。問:為徽率周幾何?
答曰:二十五步。
立天元一為徽率圓周
圓周
圓周率
取徽率
得下列方程:
即
明積演段
二十問
勾股測望
八問
;第一問:
今有直邑,不知大小,各開中門。只雲南門外二百四十步有塔,人出西門行一百八十步見塔,復抹邑西南隅行一里二百四十步恰至塔所;問邑長闊各幾何?
''答曰:長一里一百二十步,闊一里。
立天元一為邑長之半,得四次方程:
<ref>萬有文庫第二集 朱世傑撰 羅士琳草 (中) 卷下之五 四一0-四一一-</ref>。
解之得 x=240步,邑長=2x= 480b步=1里120步。
同理, 令天元一為邑闊之半
得方程:
解之得 x=180步,邑長=360步=一里。
;第七問:
今有營居山頂,岩底有泉,欲汲而不知其深。偃矩山上,令句高四尺,從矩高端望泉入下股六尺。又設重矩於上,其矩間相去一丈六尺,更從矩端望泉入上股五尺六寸。問岩深幾何?
:答曰:岩深二十二丈。
:此問與劉徽《海島算經》望深谷。
;第八問:
今有登山臨邑,不知門高。偃矩山上,令勾高三尺,斜望門額入下股四尺八寸,復望門困,入下股二尺八寸八分。復又立重矩於上,其間相去五尺。更從勾端斜望門額入股三尺六寸,又望門困入上股二尺四寸。問城門高几何?
:答曰:門高一丈。
:此問與劉徽《海島算經》|望清淵同。
或問歌彖
一十二問
茭草形段
七問
箭積交參
七問
拔換截田
 拔換截田
拔換截田一十九問
五問。
卷中《如像招數》第五問給出世界上最早的四次內插公式
今有官司依立方招兵,初招方面三尺,次招方面轉多一尺,得數為兵,今招一十五方,每人日支錢二百五十文,問兵及支錢各幾何。或問還原:依立方招兵,初招方面三尺,次招方面轉多一尺,得數為兵。今招一十五日,每人日支錢二百五十文,問招兵及支錢幾何?<br>答曰:兵二萬三千四百人,錢二萬三千四百六十二貫。<br>術曰求得上差二十七,二差三十七,三差二十四,下差六<br>求兵者,今招為上積,又今招減一為茭草底子積為二積,又今招減二為三角底子積,又今招減三為三角一積為下積。以各差乘各積,四位並之,即招兵數也。
先求出上差(一次差),二差(二次差),三差(三次差)和下差(四次差),然後求出答案,是四次插值法
招差術的運用
招兵總數=
其中
* a=上差
* b=二差
* c=三差
* d=下差
 如像招數
如像招數卷下
果垛疊藏
二十問 此章論述三角垛、三角撒星垛、四角垛、圓錐垛、芻童垛、芻甍垛。
第一問:今有三角垛果子一所,值錢一貫三百二十文,只雲從上一個值錢二文,次下層層每個累貴一文,問底子每面幾何?
:答曰:九個。
術曰:立天元一為每個底子,如積求之,得三萬一千六百八十為益實十為從方,二十一為從上廉,一十四為下廉,三為從隅,三桀方開之,得每個底子,合問。
三角垛級數:
1,2,3,4,5,6....n.
自上而下,每個果子值錢:
2,3,4,5,6.....(n+1}
三角果子垛價值V由下列級數表示
這是一個已知級數和,倒求 n 的數學問題。
朱世傑用天元術,令天元一 為每底邊的果子數 (x=n)
鎖套吞容
一十九問
方程正負
八問
雜范類會
一十三問
兩儀合轍
一十二問。。
左右逢元
二十一問。用天地二元。
三才變通
一十一問。用天,地,人三元。
四象朝元
六問,用天,地,人,物四元。
 四象朝元第二問書影
四象朝元第二問書影第二問:今有弦較和如股冪八分之三。只雲弦較較如勾弦和冪四分之一。
問二弦四勾二股三事連環得幾何?
答曰:三十步。
立天元一為勾,地元一為股,人元一為弦,物元一為開數。
得:
版本
王萱玲抄本 1819
沈欽裴細草本 1822
何元錫刊本 1822年
羅士琳細草本 1837
戴煦細草抄本 1845
志古堂刻本 1891
鴻寶齋石印本 1895
萬有文庫:朱世傑撰
羅士琳補草《四元玉鑒細草》上中下三冊 (據羅士琳1839年刊本影印)民國26年
歷代算學集成本影印 1994
傳世藏書本 1996
大中華文庫 《四元玉鑒》 Jade Mirror of the Four Unknowns 中英對照本 兩卷本 郭書春今譯 陳在春英譯 郭金海整理 遼寧教育出版社 2006
李兆華校正 《四元玉鑒》 科學出版社 2007
 萬有文庫《四元玉鑒細草》
萬有文庫《四元玉鑒細草》
 《四元玉鑒》
《四元玉鑒》 朱世傑《四元玉鑒》卷首的「古法七乘方圖」
朱世傑《四元玉鑒》卷首的「古法七乘方圖」
 四元自乘演段圖
四元自乘演段圖 四元自乘演段圖
四元自乘演段圖 立四元
立四元 四元的自乘
四元的自乘



 一氣混元
一氣混元


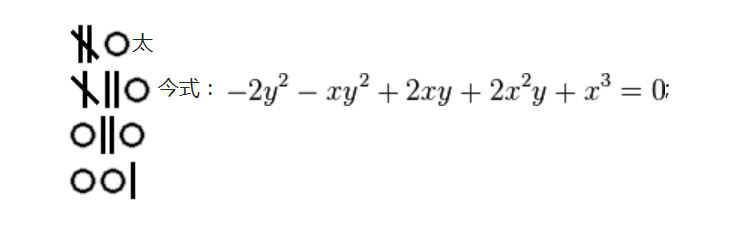 兩儀化元
兩儀化元

 雲式
雲式
 8x+4xx=0
8x+4xx=0
 2x平方+x3方
2x平方+x3方
 x=4
x=4






 三儀化圓
三儀化圓 四象會元
四象會元



 物易天位
物易天位

 今有圓城
今有圓城






 拔換截田
拔換截田

 如像招數
如像招數






 四象朝元第二問書影
四象朝元第二問書影



 萬有文庫《四元玉鑒細草》
萬有文庫《四元玉鑒細草》
