對於一個給定的數列,把它的連續兩項an+1與an的差an+1-an記為bn,得到一個新數列,把數列bn稱為原數列的一階差數列,如果cn=bn+1-bn,則數列cn是an的二階差數列依此類推,可得出數列的p階差數列,其中p∈N+
基本介紹
- 中文名:高階等差數列
- 外文名:arithmetic progression of higher order
- 學科:數學
- 定義:二階及以上的等差數列
- 性質1:前n項和Sn是關於n的p+1次多項式
- 性質2:數列的通項是關於n的p次多項式
基本知識


例題精講









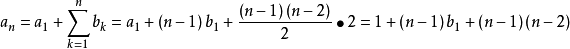
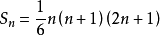













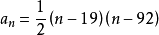

對於一個給定的數列,把它的連續兩項an+1與an的差an+1-an記為bn,得到一個新數列,把數列bn稱為原數列的一階差數列,如果cn=bn+1-bn,則數列cn是an的二階差數列依此類推,可得出數列的p階差數列,其中p∈N+











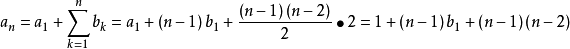
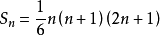













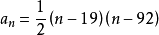
⒈定義:一般地,如果{an+1-an}是K階等差數列,就稱原數列{an}為K+1階等差數列,二階以及高於二階的等差數列統稱為高階等差數列。 [1] ...
多階等差數列又叫高階等差數列,是指二階或二階以上的等差數列。 把一個數列的所有後項與前一項之差組成一個新的數列,如果這個新的數列是普通等差數列,原數列就...
1.3數列求和1.3.1數列求和的基礎知識1.3.2數列求和的常用方法1.3.3範例解析第2章遞推數列與高階等差數列2.1數列的通項2.1.1通項公式的定義...
《數列·遞推·遞歸》是該叢書中的一種.它從數列的概念和最基本的數列——等差數列和等比數列研究開始,分別 對與等差數列、等比數列有關的差分數列、等比差數列...
所謂垛積,轉化成現代數學語言,就是一種高階的等差數列或行列式。中國古代曾經使用垛積來解對數、矩陣甚至簡單的微積分。清朝數學家李善蘭對此有較深的研究。...
如果一個數列從第2項起,每一項與它前一項的差等於同一個常數,這個數列就叫作等差數列,這個常數叫作這個等差數列的公差,記作d...
《四元玉鑒》則是中國宋元數學高峰的又一個標誌,其中最傑出的數學創造有“四元術”(多元高次方程列式與消元解法)、“垛積術”(高階等差數列求和)與“招差術...
《四元玉鑒》成書 數學家朱世傑著《四元玉鑒》成書,世傑字漢卿,號松庭,另著有《算學啟蒙》。在求解多元高次方程組、高階等差級數、高次招差法方面,公元...
本書是作者近40年對數理公式定理的研究成果,主要創立了高階等差數列的一般公式與統一通用公式,闡述了高階數列的對應項變換之性質,發明了橢圓的等值定理及其證明推導...
(4)高階等差數列(1572―1585) (5)調和數列(15861596) (6)循環數列(1597―1617) 第九章 排列和組合 1.有關排列數和組合數的運算和證明 (1)含組合數的方程...
《四元玉鑒》則是中國宋元數學高峰的又一個標誌,其中最傑出的數學創造有“四元術”(多元高次方程列式與消元解法)、“垛積術”(高階等差數列求和)與“招差術...
遞歸的方法可以依次定義各階等差數列:對於數列{an},如果{an+1-an}是r階等差數列,則稱數列{an}是r+1階等差數列.二階或二階以上的等差數列稱為高階等差數列...
1665年,牛頓把二項式定理推廣到n為分數與負數的情形,給出了展開式。 二項式定理在組合理論、開高次方、高階等差數列求和,以及差分法中有廣泛的套用。 [1] ...
42.3高階等差數列(291)習題42(293)第43講面積坐標(Ⅰ)(294)43.1面積坐標的定義(294)43.2例題(296)43.3直角坐標與面積坐標之間的轉換(298)習題43(298)...
第一節 數列一、等差數列與等比數列三、高階等差數列與等比數列三、遞推數列與周期數列四、數列的求和五、數列的性質第二節 不等式...
6, 高階等差數列及其代數性質, 1998, 《青海民族師專學報》。7, 漢藏機器翻譯中複句的翻譯規則, 2006.11, 《中文信息處理前沿進展》。...
畢達哥拉斯研究多角數是結合圖形來說的,而尼科馬霍斯則完全脫離了幾何圖形,只借用了幾何名稱,實際此問題可歸人高階等差數列的範疇.第21章後研究幾何級數、算術...
此外他還創造出“垛積法”,即高階等差數列的求和方法,與“招差術”,即高次內插法。主要著作是《算學啟蒙》與《四元玉鑒》。...
堆垛計算與高階等差數列求和廢鋼鐵回收與等比數列求和恆等式能舉例證明嗎第七章 不等式與近似計算 近似與精確不等式的妙用不等式與連分數...
《四元玉鑒》則是中國宋元數學高峰的又一個標誌,其中最傑出的數學創造有“四元術”(多元高次方程列式與消元解法)、“垛積術”(高階等差數列求和)與“招差術...
