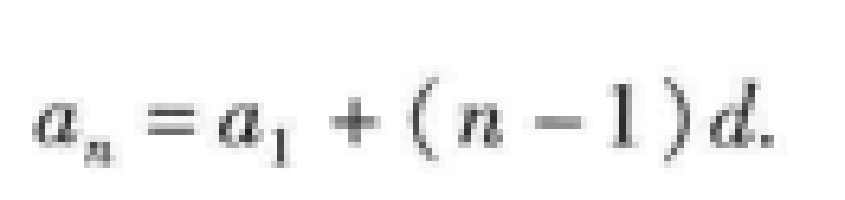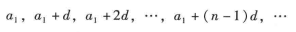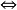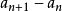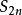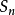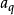公差(數理科學概念)

如果一個數列從第2項起，每一項與它前一項的差等於同一個常數，這個數列就叫作等差數列，這個常數叫作這個等差數列的公差，記作d．

基本介紹

• 中文名：公差
• 外文名：Common difference
• 所屬領域：數理科學
• 性質：等差數列的參數

定義

從第二項起,每一項都等於前一項加上同一個數d的有限數列或無限數列.又叫算術數列.這個數d稱為等差數列的公差.等差數列可以記作

等差數列從第二項開始每一項是前項和後項的算術平均數.
如果等差數列的公差是正數,則該等差數列是遞增數列;

如果等差數列的公差是負數,則該數列是遞減數列;

如果等差數列的公差等於零,則該數列是常數列.
對於一個數列a_l,a₂,…,a_n,…,如果它的相鄰兩項之差a₂-a₁,a₃-a₂,…,a_n+1-a_n,…構成公差不為零的等差數列,則稱數列{a_n}為二階等差數列. 運用遞歸的方法可以依次定義各階等差數列:對於數列{a_n},如果{a_n+1-a_n}是r階等差數列,則稱數列{an}是r+1階等差數列.二階或二階以上的等差數列稱為高階等差數列.
r階等差數列的通項公式可以用一個關於項數n的r次多項式來表示,反之,通項公式為項數n的r次多項式的數列必為r階等差數列.
高階等差數列的求和方法主要有兩種,一種是將其通項(項數n的r次多項式)表成差分多項式的線性組合從而求和.另一種是利用自然數冪的求和公式,如

r階等差數列的前n項和公式是項數n的r+1次多項式,對r不太高的情況也可用待定係數法來確定.
二階等差數列的通項

式中a_n是第n項,a₁是第一項,n為項數,d₁是數列的後項減去緊鄰的前一項所得的第一次差構成的數列的首項,d₂是第二次差.例如二階等差數列1,4,9,16,25,36,49,…,通項

二階等差數列錢n項和

例如二階等差數列{n^2}前n項和

{ }是等差數列 =常數d，d為等差數列{ }的公差．

相關公式

設{ }是等差數列，d為等差數列{ }的公差，則有如下公式：

等差數列的通項公式：

等差數列的一般形式：

等差數列的前n項和公式：

相關性質

(1)常數列：C，C，…，C是公差d=0的等差數列．

(2)等差中項：如果a，A，b成等差數列，則A叫作a與b的等差中項，且A=(a+b)/2．

(3)若Sn是等差數列的前n項和，則Sn， 一 ， - ，…是一個等差數列．

(4)若{ }是等差數列，公差d>0時{ }是遞增數列，d<0時{ }是遞減數列．

(5)在同一數列中，當m+n=p+q時， + = + ．