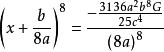一元八次方程指根據阿貝爾定理，≥5次的方程無根式解，而對於些特殊的方程來說，一定有根式解。註：當前的求根公式沒有經過嚴格的數論推導，僅在特殊的八次方程中可以使用。
基本介紹
- 中文名：一元八次方程
- 性質：方程式
- 對象：特殊的方程
- 學科：數學
公式,推導過程,化簡過程,
公式
ax8+bx7+cx6+dx5+ex4+fx3+gx2+hx+j=0
重根判別式：A=16ac-7b2 B=7bd-4c2 C=56ae-5c2
D=28af-cd E=112ag-d2 F=1225bh-16e2
G=4900aj-e2
當A=B=C=D=E=F=0時，
推導過程
（x+
）8=x8+(b/a)x7+(7b/16a)x6+(7b/64a)x5+(35b/2048a)x4+(7b/4096a)x3+(7b/65536a)x2+(b/262144a)x+(b/16777216)
原方程兩邊同時除以a，按照次數同位相減，作差，分子即化簡前的重根判別式。
化簡過程
64a2d-7b3=64d×（49b4÷256c2）-7b3=7bd-4c2，其餘相同，即可得到當A=B=C=D=E=F=0時，
