根式

根式是數學的基本概念之一，是一種含有開方(求方根)運算的代數式，即含有根號的表達式。按根指數是偶數還是奇數,根式分別稱為偶次根式或奇次根式。

基本介紹

• 中文名：根式
• 外文名：radical expression
• 類型：代數運算
• 所屬學科：數學
• 分類：偶次根式、奇次根式

定義

設正整數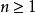，已知數a，若有數x滿足，則稱x為a的n次方根，記為當n=2時，記為 ，作為代數式，稱為根式，n稱為根指數，a稱為根底數。在實數範圍內，負數不能開方，一個正數開偶次方有兩個根，其絕對值相等，符號相反。

根式的性質

①

②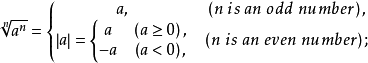

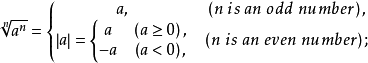
③

④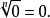

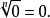
n次算術根

若,則稱為a的n次算數根。算術根是唯一的，且是非負數的非負方根。

同次根式

跟指數相同的根式。只有同次根式才能進行乘、除運算。

同類根式

被開方數相同、根指數也相同的根式。只有同類根式才能進行加、減運算。

根式的運算法則

①

②

③

④

⑤其中.

最簡根式

當根式滿足以下三個條件時，稱為最簡根式。

①被開方數的指數與根指數互質；

②被開方數不含分母，即被開方數中因數是整數，因式是整式；

③被開方數中不含開得盡方的因數或因式。

分母有理化

又稱“有理化分母”，是指通過適當的變形划去代數式分母中根號的運算。

一般情況下，在進行根式運算及把一個根式化成最簡根式時，都要將分母有理化，兩個含有根式的代數式相乘，如果它們的積不含根號，我們就說這兩個代數式互為有理化因式。