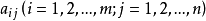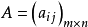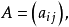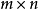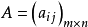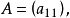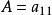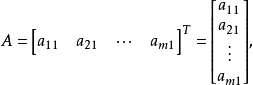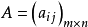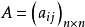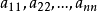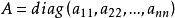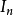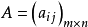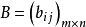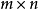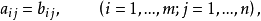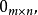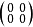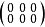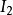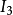基本介紹
矩陣的定義
由m×n個數
排成一個m行n列的矩形表,稱為m行n列
矩陣,記作
其中
叫做矩陣A的第i 行第j 列元素,i,j 稱為足標。矩陣的元素簡稱元,可以是
實數、
複數或
變數函式。元素是實數的矩陣稱為
實矩陣,元素是複數的矩陣稱為
復矩陣.
(1)式也可記為
或
為一個m行n列矩陣,簡稱
矩陣,寫在前面的字母m表示A的行數,寫在後面的字母n表示A的列數。
行矩陣和列矩陣
稱之為
行矩陣,或
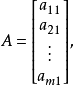
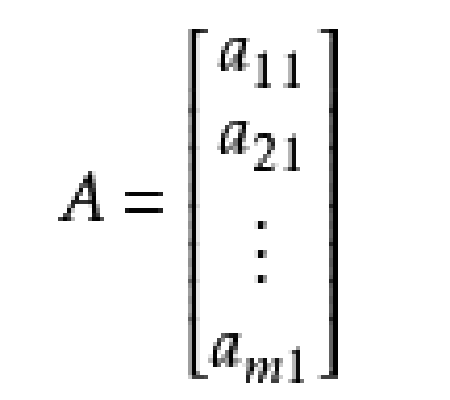
行向量。同樣,若A只有一列,即n=1,這時
稱之為
列矩陣或
列向量,當m=n=1時,A只有一個元素
這時我們就把A看成是數,即
。
為方便起見,我們有時把列矩陣橫轉來寫,但用花括弧表示,或仍用方括弧,但在右上角加上轉置符號T,即
行矩陣的
轉置矩陣是列矩陣,列矩陣的轉置矩陣是行矩陣。
相關概念
零矩陣
所有元素都是零的矩陣,叫
零矩陣,記為
,(注意這裡的
表示一個矩陣,不是數零)必要時可記為
表明是一個m行n列的
零矩陣。
方陣
對角陣
若一個方陣除了主對角線上的元素外,其餘元素都等於零,則稱之為對角陣,其形狀為
單位陣
主對角線元素全為1的n階對角陣,稱為
單位陣,記為
:
三角陣
主對角線以下元素都為零的方陣,稱為上三角陣,即
可見,對角陣既是上三角陣,又是下三角陣。
矩陣的相等
若
,
都是
矩陣,(我們稱它們是同型的),並且每個對應元素都相等,即
注意,不同型的零矩陣或
單位陣,都是不相等的,例如:
與
;
與
都不相等。