基本介紹
- 中文名:多重信號分類
- 外文名:MUSIC(MUITILY SIgnal Classification)
- 套用:空間譜估計、信號分離、DOA估計
- 發明人:Schimidt R O等人
- 發明時間:1979年
算法意義
假設基礎
MUSIC算法
經典MUSIC算法

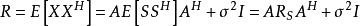

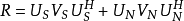










算法步驟
- 由陣列的接收數據得到數據協方差矩陣;
- 對協方差矩陣進行特徵分解;
- 由協方差矩陣的特徵值進行信號源數判斷;
- 確定信號子空間和噪聲子空間;
- 根據信號參數範圍進行譜峰搜尋;
- 找出極大值點對應的角度就是信號入射方向。

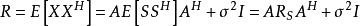

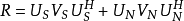










音樂是反映人類現實生活情感的一種藝術(英名稱:music;法文名稱: musique;義大利文:musica)。音樂可以分為聲樂和器樂兩大類型,又可以粗略的分為古典音樂、民間音樂、...
music可以指: 中文釋義音樂:一種很抽象的藝術形式。 通信中常用的music算法:也就是英文Multiple Signal Classification的簡稱,多信號分類算法。 中文的解釋就是音樂的...
流行音樂是根據英語Popular Music翻譯過來的。流行音樂準確的概念應為商品音樂,是指以盈利為主要目的而創作的音樂。它是商業性的音樂消遣娛樂以及與此相關的一切“...
輕音樂又名“情調音樂”,指流行音樂(準確的概念應為商品音樂,即以贏利為主要目的創作的音樂)中的器樂作品,不包括搖滾樂、迪斯科等節奏強烈的音樂。 輕音樂以通俗...
音樂領域中,獨立音樂(Independent Music,簡稱Indie music或Indie),或稱硬地音樂,用來描述有別於主流商業唱片廠牌所製作的音樂。顧名思義,獨立音樂的製作過程獨立自主...
雖然現在大家似乎傾向將“純音樂”甚至Absolute music理解為“不包含填詞的音樂”,但Absolute music的本意是“絕對音樂”,或者“純音樂”,與“標題音樂”相對,即為...
對於聽眾來說,音樂表演不但是欣賞、理解音樂內容與形式的必要手段,也可以從不同音樂表演的比較中欣賞、鑑別、認識由於表演者對樂曲的不同解釋而被強調的音樂的某些...
巴洛克音樂的一些特點(Baroque),它的節奏強烈、跳躍,採用多旋律、複音音樂的復調法,比較強調曲子的起伏,所以很看重力度、速度的變化。巴洛克音樂是後期發展的一個...
MUSIC算法是一種基於矩陣特徵空間分解的方法。從幾何角度講,信號處理的觀測空間可以分解為信號子空間和噪聲子空間,顯然這兩個空間是正交的。信號子空間由陣列接收到...
即曲風。音樂風格是指在音樂範疇中各種音樂要素——曲調、節奏、音色、力度、和聲、織體和曲式等富有個性的結合方式,但主要指的是曲調。這些要素的特殊結合方式能...
雷鬼音樂是一種由斯卡(Ska)和洛克斯代迪(Rock Steady)音樂演變而來的牙買加流行音樂,也譯作雷吉,雷蓋。事實上,很難在洛克斯代迪和雷鬼之間劃出明確的界限。只是後者...
音樂學院是指專門從事音樂藝術類教育和研究的高等院校,是培養和繼承音樂專業技能的技術人才的搖籃。 中國現有十一所獨立設定的高等音樂院校:上海音樂學院、中央音樂...
唱片是一種音樂傳播的介質概括。唱片的物質形態可以分為早期的鋼絲唱片、膠木78轉唱片、黑膠唱片及今時今日的CD光碟等等。 隨著計算機網際網路的快速普及,更多人傾向於...
新世紀音樂是介於電子音樂和古典音樂之間的新樣式,也有譯作新紀元音樂的。是一種在上個世紀70年代後期出現的一種音樂形式,由於其豐富多彩、富於變換,不同於以前...
廣義的講,音樂就是任何一種藝術的、令人愉快的、審慎的或其他什麼方式排列起來的聲音。所謂的音樂的定義仍存在著激烈的爭議,但通常可以解釋為一系列對於有聲、無聲...
歐美音樂(Western music),泛指來源於西方國家(歐美地區,一般意義上包括北美、拉丁美洲、歐洲、大洋洲)的音樂,歌曲語言多以英語、法語、西班牙語、俄語等為主。其中...
一種音樂類別的名稱。當中國古典音樂流瀉而出的一剎那間,你可以體悟到空氣中流動的是高山、是流水、是絲竹、是冬雪,是千古纏綿不絕的生命呼喚。那份說不清、道...
《音樂遊戲》(Music Game)是使模擬器(或鍵盤)發出相應的音效的遊戲。《音樂遊戲》不斷出現的各種按鍵(NOTE)合成一首歌曲,類似於奏樂。這類遊戲主要考的是你對...
中國傳統音樂是在以黃河流域為中心的中原音樂和四域音樂以及外國音樂的交流融合之中形成發展起來的。因此可以說,中原音樂、四域音樂、外國音樂是中國傳統音樂的三大...
在音樂領域,“modernist”這個術語一般指出現在20世紀初左右的音樂語言上的重要分離,在和聲、旋律、音響效果和節奏方面的音樂觀念里創造出一系列新的理解的音樂語言。...
G-MUSIC是台灣最大的兩家唱片銷售商玫瑰唱片和大眾唱片於2002年6月由和信集團併購之後建立的台灣最大的唱片銷售股份有限公司,在G-MUSIC成立之初,擁有海量的音樂資源...
《Music S.T.A.R.T!!》是日本偶像組合μ's推出的第六張單曲專輯,收錄有四首歌曲(兩首是Off Voice版本)和三部廣播劇。發售於2013年11月27日,首周即登上...
音樂術語是指在音樂表演中用來指導演奏者表演的專業術語。其中既包括音樂構成要素(如速度、表情、強弱、調式、和聲、旋律等),也包括音樂的時期與流派(如中世紀時期、...
music是一個英語單詞,可以用作名詞,可以翻譯為音樂、樂曲,等等。... music是一個英語單詞,可以用作名詞,可以翻譯為音樂、樂曲,等等。 中文名 音樂 外文名 music ...
中國音樂,文獻一般追溯到黃帝時代,據考古發現,中國音樂可追溯至7000多年前,中華民族在幾千年的歷史長河中,創造了豐富的音樂文化。中國音樂曾經對中國周邊地區的音樂...
音樂類別 本詞條是多義詞,共2個義項 展開 某個民族在古代或者近代時期創作帶有自己民族風格的歌曲,是指每個民族的傳統歌曲,每個民族的先民都有他們自古代已有的歌...
