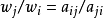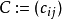嘉當矩陣

在數學中，嘉當矩陣是由法國數學家埃利·嘉當引入的一類特別矩陣，最大的套用在於李代數的分類理論。在有限維代數的表示理論中，嘉當矩陣另有其它意義。

基本介紹

• 中文名：嘉當矩陣
• 外文名：cartan matrix
• 提出者：法國數學家埃利·嘉當
• 套用學科：數學
• 套用領域：李代數的分類理論
• 性質：對角線上的項等於二

李代數

所謂廣義嘉當矩陣是具有下述性質的方陣：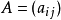

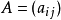
各項皆為整數：。

對角線上的項等於二：。

非對角線項非正：

。

存在正對角方陣D 使 A 可以寫成 ，其中 S 是對稱方陣。

第四個條件可由第一及第五個條件導出。在第五個條件中，若可取 S 為正定，則稱 A為嘉當矩陣。

若兩個嘉當矩陣差一個排列矩陣的共軛：，則稱兩者同構。若一嘉當矩陣同構於分塊對角的嘉當矩陣，則稱之為可化的，反之則稱為不可化。

由半單李代數可以得到根系，對應的廣義嘉當矩陣定義為

其中 是選定的單根。單李代數對應於不可化嘉當矩陣。

不可化嘉當矩陣可透過連通丹金圖分類。具體方式是取 n 個頂點（n 為嘉當矩陣 A 的階數），將頂點 i,j以條邊相連。定義每個頂點的權 使得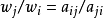，若兩個相鄰頂點 i,j 的權不同，則規定邊從權大者指向小者。這套模式類似於從根系定義丹金圖的手法。

表示理論

對於域 F上的有限維結合代數 A，考慮不可約、 F-有限維左 A-模，對每個 ，存在唯一的不可分解左射影模（至多差一個同構），使得 。取為 在的合成列中作為合成因子的重數。方陣 稱為 A的嘉當矩陣。