整表示是一類特殊的線性表示。設R是一個整環,其分式域為F,若群G在域F上的一個矩陣表示使得對任g∊G,矩陣T(g)的每個元素均在R中,則稱這種表示為整表示。若R是一個主理想整環,其分式域為F,則每個F表示均等價於一個R表示。
基本介紹
- 中文名:整表示
- 外文名:integral representation
- 適用範圍:數理科學
簡介
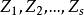
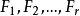
分解數
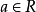
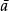
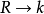
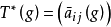
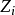
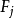
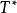
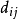
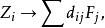
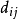
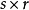
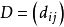
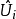
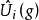
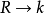
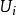

整表示是一類特殊的線性表示。設R是一個整環,其分式域為F,若群G在域F上的一個矩陣表示使得對任g∊G,矩陣T(g)的每個元素均在R中,則稱這種表示為整表示。若R是一個主理想整環,其分式域為F,則每個F表示均等價於一個R表示。
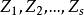
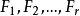
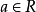
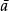
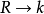
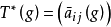
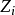
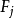
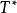
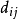
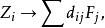
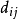
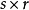
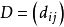
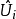
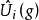
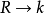
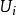
整表示是一類特殊的線性表示。設R是一個整環,其分式域為F,若群G在域F上的一個矩陣表示使得對任g∊G,矩陣T(g)的每個元素均在R中,則稱這種表示為整表示...
整整,漢語辭彙。注音:zhěng zhěng。釋義:(1).整齊嚴謹貌;(2).工整;(3).達到一個整數的,實足的。...
中文名稱 整合表達 英文名稱 integrant expression 定義 基因整合到基因組中發生的表達。 套用學科 遺傳學(一級學科),分子遺傳學(二級學科) 以上內容由全國科學...
端整是一個漢語詞語,拼音是:duān zhěnɡ,釋義:1、是指端莊整齊。2.備辦;收拾。...... 劉溫 《賀新郎》詞:“玻璃三萬六千頃,洗精神,塵埃盡絕,夐然端整...
節整是漢語辭彙,讀音是jié zhěng,出自《後漢書·鄭均傳》。...... 節整是漢語辭彙,讀音是jié zhěng,出自《後漢書·鄭均傳》。中文名 節整 拼音 jié zhěng...
治整,讀音為zhì zhěng,是一個漢語詞語,意思是嚴整。...... 治整,讀音為zhì zhěng,是一個漢語詞語,意思是嚴整。中文名 治整 拼音 zhì zhěng 注音 ㄓ...
新整 嶄新完整;嶄新整齊。《紅樓夢》第六五回:“衣裳不如意,不論綾緞新整,便用剪子鉸碎,撕一條,罵一句。”清 王韜 《淞隱漫錄·諸曉屏》:“既過小橋,...
茶葉感官審評術語 勻整(evenly)上中下三段茶的粗細、長短、大小較一致,比例適當,無脫檔現象。 出處 清馮班 《鈍吟雜錄》卷六:“唐宋 人碑上行書,亦自勻整。...
打整 拼音:dǎ zhěng 注音:ㄉㄚˇㄓㄥˇ引證解釋1. 準備;整理。2. 發落;懲治。...... 打整 拼音:dǎ zhěng 注音:ㄉㄚˇㄓㄥˇ引證解釋1. 準備;整理...
錢整原名錢成,因避明成祖諱改錢整,五代十國時期吳越國國王錢鏐第二十五世孫,淮安府山陽縣滿蒲坊人,為吳越錢氏江北後裔始祖。自幼習武、謀略出眾,青年時期被...
