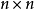共軛類

數學上，特別是在群論中，群的元素可以分割成共軛類（Conjugacy class）；同一個共軛類的元素有很多共同的屬性，而且研究非交換群的共軛類可以看出很多關於它們的結構的重要特徵。對於交換群，這個概念是平凡的，因為每個類就是一個單元素集合。

在同一個共軛類上取常值的函式稱為類函式。

基本介紹

• 中文名：共軛類
• 外文名：conjugacy classes
• 相關術語：類函式
• 套用學科：數學
• 套用領域：群論
• 定義：群的元素可以分割成共軛類

定義

設G為群。對於G中共軛的兩個元素a和b，必存在G中一個元素g，滿足

• gag^{-1}=b。
  

（線上性代數中，這叫做相似變換。）

很容易證明共軛是等價關係，因此將G分割為等價類。（這表示群的每個元素屬於恰好一個共軛類，而類Cl(a)和Cl(b)相等若且唯若a和b共軛，否則不相交。）包含元素a屬於G的等價類是

• Cl(a) = {gag:g∈G}
  

並稱為a的共軛類。G的類數是共軛類的個數。

例子

對稱群S₃，由所有3個元素的6個置換組成，擁有三個共軛類：

• 恆等 (abc -> abc)表示為(1)
  
• 對換 (abc -> acb，abc -> bac，abc -> cba)表示為(23) (12) (13)
  
• 三階輪換 (abc -> bca，abc -> cab)表示為(132) (123)
  

對稱群S₄，由4個元素的全部24個置換組成，有5個共軛類：

• 恆等
  
• 對換
  
• 三階輪換
  
• 四階輪換
  
• 雙對換
  

參看立方體的恰當轉動，它可以用體對角線的枚舉刻劃。

在矩陣，在同一個共軛類的矩陣稱為相似矩陣。

屬性

• 單位元總是自成一類，也就是說Cl(e) = {e}
  
• 若G可交換，則gag=a對於所有a和g屬於G成立；所以Cl(a) = {a}對於a屬於G成立；可見這個概念對於交換群不是很有用。
  
• 若G的兩個元素a和b屬於同一個共軛類（也即，若它們共軛），則它們有同樣的階。更一般地講，每個關於a的命題可以轉換成關於b=gag的一個命題，因為映射φ(x) =gxg是一個G的自同構。
  
• G的一個元素a位於G的中心Z(G)若且唯若其共軛類只有一個元素，a本身。更一般地講，若C_G(a)代表G中的a的中心化子，也即，有所有滿足ga=ag的元素g組成的子群，則指數[G: C_G(a)]等於a的共軛類中元素的個數。
  

共軛類方程

定義

若G為有限群，則上節的內容，加上拉格朗日定理，可以得出如下結論：每個共軛類的元素個數整除G的階。

進一步的有，對於任何群G，可以通過從G的每個元素個數大於1的共軛類中取出一個元素來定義一個代表集S= {x_i}。則G是Z(G)和S的元素的共軛類Cl(x_i)的不交並集。由此可以寫出重要的類方程：

• |G| = |Z(G)| + ∑_i[G:H_i]
  

其中求和取遍對於每個S中的x_i的H_i= C_G(x_i)。注意[G:H_i]是共軛類i的元素個數，一個|G|的大於1的除數。如果|G|的除數已知，則該方程經常用於獲得關於共軛類或者中心的大小的信息。

例子

考慮一個有限p-群G（也即，次數為p的群，其中p是一個素數而n> 0）。我們將證明：每個有限p-群有非平凡的中心。

因為G的任意子群的次數必須整除G的次數，所以每個H_i也是某個冪p。但是類方程要求|G| =p= |Z(G)| + ∑_i(p)。因此我們可以看出p必須整除|Z(G)|，所以|Z(G)| > 1。

子群的共軛

更一般的來講，給定任意G的子集S（S不必是子群），我們定義一個G的子集T為S的共軛，若且唯若存在某個g屬於G滿足T=gSg。我們可以定義Cl(S)為所有共軛於S的子集T的集合。

一個常用的定理是，給定任意子集S，N(S)（S的正規化子）的指數等於Cl(S)的次數：

• |Cl(S)| = [G: N(S)]
  

這是因為，如果g和h屬於G，則gSg=hSh若且唯若gh屬於N(S)，換句話說，若且唯若g和h屬於N(S)的同一個陪集。

注意這個公式推廣了前面關於共軛類元素的個數的定理（S= {a}的特殊情況）。

上述定理在討論G的子群時尤其有用。子群可以由此分為等價類，兩個子群屬於同一類若且唯若它們共軛。共軛子群是同構的，但是同構子群未必共軛（例如，交換群可以有兩個不同的互相同構的子群，但是它們不可能共軛）。

作為群作用

如果對於任意兩個G中的元素g和x定義

• g.x=gxg
  

則我們有了一個G在G上的群作用。該作用的軌道就是共軛類，而給定元素的定點子群就是該元素的中心化子。

同樣，我們可以定義一個在G的所有子群或者所有子集的集合上的G的群作用如下

• g.S=gSg。