陪集是指H是群G的子群,對於某一g∈G,{gh|對於所有h∈H}表示H的一個左陪集,記作gH;{hg|對於所有h∈H}表示H的一個右陪集,記作Hg;也譯作傍系,旁集等。
基本介紹
- 中文名:陪集
- 外文名:Coset
- 學科:代數
- 分類:左右陪集
- 別稱:傍系,旁集
- 相關名詞:阿貝爾群
簡介
舉例
C2
整型
矢量
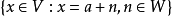
陪集是指H是群G的子群,對於某一g∈G,{gh|對於所有h∈H}表示H的一個左陪集,記作gH;{hg|對於所有h∈H}表示H的一個右陪集,記作Hg;也譯作傍系,旁集等。
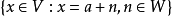
陪集是指H是群G的子群,對於某一g∈G,{gh|對於所有h∈H}表示H的一個左陪集,記作gH;{hg|對於所有h∈H}表示H的一個右陪集,記作Hg;也譯作傍系,旁集等...
定義 重陪集((double coset)亦稱雙陪集.群中元素依賴於兩個子群的一種等價類.設G是一個群,H,K是它的兩個子群(不必相異),二為G中固定元.記HxK={hxk}hEH...
陪集表((coset table)描述群G中某個有限指數子群H在G中的全部陪集的表.設G由g},gz}…,g尹生成,H是G中一個指數為m的子群.H在G中的陪集表T是一個mX2r...
陪集計數(coset enumeration)亦稱托德一考克斯特算法一種群論算法.求有限表現群中子群指數的一種算法.設 是一個有限表現群.對於由}mgz}...,g:的字二,,二:,...
《氏函式中的手征反常項和陪集純規範場的研究》是一部出版的論文,作者是井思聰。...... 《氏函式中的手征反常項和陪集純規範場的研究》是一部出版的論文,作者...
拉格朗日定理是群論的定理,利用陪集證明了子群的階一定是有限群的階的約數值。1.定理內容敘述:設H是有限群 的子群,則 的階整除 的階。...
因為我們從一個群和正規子群得到的最終的商包含比只是陪集的(正常除法所產生的)數目要更多的信息,這裡得到了一個群結構自身。商群例子 考慮整數集 Z (在加法下...
設G是一個群 ,H是其子群。 若H的左陪集與右陪集總是相等(對任何的a∈G,aH=Ha), 則稱H是G的正規子群或不變子群,記為H⊴G。注:(1) 任何群G都有...
生成子群的陪集。對於被認為是無向的凱萊圖,頂點連通性等於這個圖的度。 [2] Cayley圖陪集圖 編輯 如果轉而把頂點作為固定子群 的右陪集,就得到了一個有關的...
1 理論介紹 2 定義 3 例子 4 陪集定理 5 準齊性質 6 物理原理 齊性空間理論介紹 編輯 在數學,特別是李群、代數群與拓撲群的理論中,關於群G的一個齊性...
《分子振動的混沌理論》是2003年科學出版社出版的圖書,作者是吳國禎。本書系統地介紹了如何運用李代數、李群的陪集空間表示方法來研究分子高激發振動態的非線性動力...
由正規子群的陪集組成的一種群。設H是群G的一個正規子群,G關於H的所有左陪集所成的集合G/H={xH|x∈G}按照如下的乘法:(xH)(yH)=(xy)H成為一個群,稱...
,即S的所有共軛子集與 關於 的所有陪集間可建立雙射。[1] 證明 令是中含的共軛子集類(即與共軛的全體子集),再令若 ,則便有 ,從而...
商模(quotient module)是模論的重要概念之一,模M與它的商模M-之間的性質有著密切的聯繫。它是將A模M的元素進行陪集分類後所得到的新模,亦稱“差模”。設是...
2.6.3陪集與解碼方法89小結92習題92第3章環943.1環的定義及其性質953.1.1環的定義953.1.2環的性質973.1.3整環993.1.4除環101...
