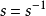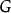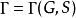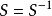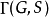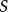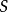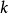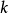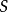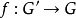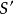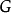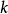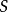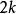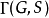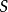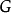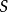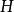基本介紹
- 中文名:Cayley圖
- 外文名:Cayley graph
- 別稱:凱萊圖
定義,例子,特徵,基本性質,陪集圖,與群論的關係,參見,
定義
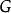
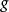
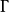
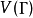




對於任何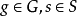 ,對應於元素
,對應於元素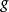 ,和
,和 ,的頂點用顏色
,的頂點用顏色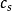 ,的有向邊連線。因此邊集合
,的有向邊連線。因此邊集合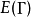 ,由形如
,由形如 ,的有序對構成,帶著
,的有序對構成,帶著 提供的顏色。
提供的顏色。
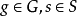

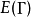


例子
假設G=Z是無限循環群而集合S有標準生成元1和它的逆元(用加法符號為−1)構成,則它的凱萊圖是無窮鏈。 圖1.二面體群D4在兩個生成元a和b上的凱萊圖。
圖1.二面體群D4在兩個生成元a和b上的凱萊圖。
 圖1.二面體群D4在兩個生成元a和b上的凱萊圖。
圖1.二面體群D4在兩個生成元a和b上的凱萊圖。類似的,如果G=Zn是n階循環群而S由兩個元素構成,G的標準生成元和它的逆元,則凱萊圖是環圖Cn。
二面體群D4在兩個生成元a和b上的凱萊圖列於右側。紅色箭頭表示左乘元素a。因此元素b是自我逆轉的,表示左乘元素b藍色線是無方向的。因此這個圖是混合的:它有8個頂點,8個有向邊,4個邊。群D4的凱萊表可以從群展示得出:

在對應於集合S= {a,b,a,b}的兩個生成元a,b上的自由群的凱萊圖列出在文章開頭,這裡的e表示單位元。沿著邊向右走表示右乘a,而沿著變向上走表示乘以b。因為自由群沒有關係,它的凱萊圖中沒有環。這個凱萊圖是證明巴拿赫-塔斯基悖論的關鍵因素。
特徵
群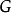 通過左乘作用在自身上(參見凱萊定理)。這個作用可以看作
通過左乘作用在自身上(參見凱萊定理)。這個作用可以看作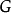 作用在它的凱萊圖上。明顯的,一個元素
作用在它的凱萊圖上。明顯的,一個元素 映射一個頂點
映射一個頂點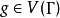 到頂點
到頂點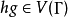 。凱萊圖的邊集合被這個作用所保存:邊
。凱萊圖的邊集合被這個作用所保存:邊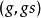 變換成邊
變換成邊 。任何群在自身上的左乘作用是簡單傳遞的,特別是凱萊圖是頂點傳遞的。這導致了凱萊圖的下列特徵:
。任何群在自身上的左乘作用是簡單傳遞的,特別是凱萊圖是頂點傳遞的。這導致了凱萊圖的下列特徵:
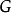
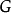

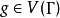
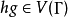
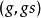

圖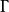 是群
是群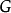 的凱萊圖,若且唯若它通過圖自同構許可
的凱萊圖,若且唯若它通過圖自同構許可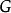 的簡單傳遞作用(就是保存邊的集合)。
的簡單傳遞作用(就是保存邊的集合)。
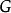
要從一個凱萊圖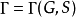 恢復群
恢復群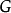 和生成集
和生成集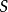 ,選擇一個頂點
,選擇一個頂點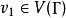 並標記上這個群的單位元。接著對每個
並標記上這個群的單位元。接著對每個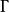 的頂點
的頂點 標記上變換
標記上變換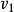 到
到 的
的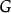 的唯一元素。產生
的唯一元素。產生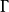 為凱萊圖的
為凱萊圖的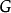 的生成元的集合
的生成元的集合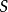 是毗連到選擇的頂點的頂點的標記的集合。生成集合是有限(這是凱萊圖的共同假定)若且唯若這個圖是局部有限的(就是說每個頂點毗連與有限多個邊)。
是毗連到選擇的頂點的頂點的標記的集合。生成集合是有限(這是凱萊圖的共同假定)若且唯若這個圖是局部有限的(就是說每個頂點毗連與有限多個邊)。
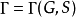
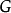
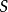
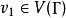
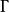

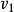

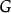
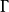
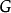
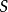
基本性質
如果生成集合的成員 是自身的逆元,即
是自身的逆元,即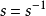 ,則它一般被表示為無向邊。
,則它一般被表示為無向邊。