基本介紹
- 中文名:群作用
- 外文名:Group Action
- 領域:數理科學
- 套用:抽象代數;集合
定義






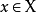
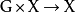
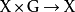

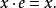



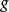


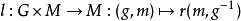
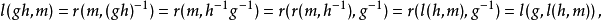
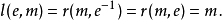
群作用軌道
1.作用軌道

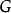

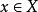


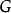


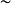
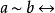
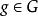

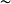
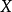
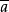
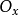
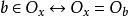
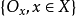
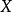

2.穩定子群

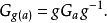
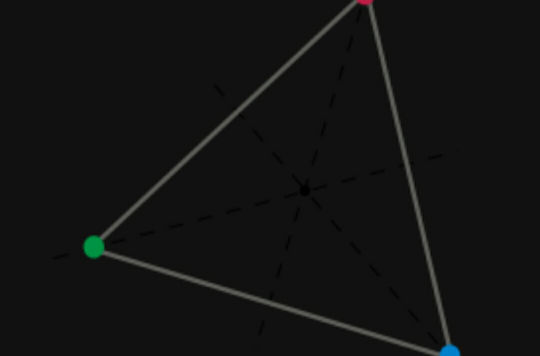






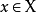
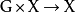
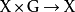

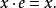



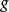


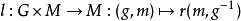
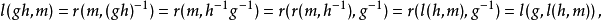
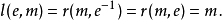

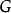

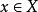


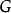


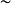
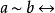
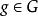

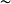
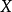
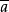
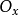
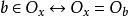
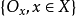
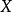


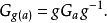
數學上,對稱群描述物體的所有對稱性。這是通過群作用的概念來形式化的:群的每個元素作為一個雙射(或者對稱作用)作用在某個集合上。在這個情況下,群稱為置換群(...
2014年6月9日,成都市城鄉房產管理局以成房發〔2014〕97號印發《關於發揮民眾作用做好居民自治改造工作的指導意見》。該《意見》分基本含義、適用範圍、基本原則、...
群體功能(group function)是指群體對組織和個人所起的社會作用。對組織而言,正式群體的主要功能是完成組織分配的任務,以保證組織目標的實現,其組織維繫功能是次要的...
生物生產力是生態系統提供生物產品高低的一種性能,它既是生態系中能量流動和物質循環這兩大功能的綜合表征,又是生物種群通過同化作用生產或積累有機質的能力。群落...
人民民眾是一個歷史範疇,是指一切對社會歷史起著推動作用的人們。在階級社會中,它包括一切對歷史發展起著促進作用的階級、階層和社會集團。人民民眾這個概念在不同...
EM菌原液滲入水體後,其群體作用能殺死或抑制病原微生物和有害物質,調整養殖生態環境,增加水中溶氧量(氧氣),促進養殖生態系中的正常菌群和有益藻類活化生長,保持...
高可用集群的套用系統有多樣化發展趨勢,用途也越來越多樣化,同時帶來了配置及可...(HA cluster)是指如單系統一樣地運行並支持(計算機)持續正常運行的一個主機群...
家庭是人類最早和最基本的社會群體形式,它對人類社會的發展起著十分重要的作用。...土著人那裡來的,由共妻的一群丈夫互稱“普那路亞”;共夫的一群妻子也互稱“...
推廣通過結合各種網路行銷方式來進行電子商務推廣,才能起到更好、更長久的作用。...QQ 群通訊、論壇社區發帖、攢寫軟文宣傳、活動推廣、網路廣告投放等,對每一種...
益生菌通過調理人體腸道菌群,產生一些有益物質直接起作用。益生元保健功效 益生元被明確的制定作用於大腸菌落。以下為已經發表功效:...
“團體動力學”這個概念,藉以標明他要對團體中各種潛在動力的互動作用,團體對...心理環境主要是安全感;社會環境則是群體中的次文化或小群體以及群體外的城鄉風土...
以表達白細胞介素2(IL-2)和γ干擾素(IFN-γ)為主的TH1群細胞,可以增強殺傷細胞的細胞的毒性作用,激發遲髮型超敏反應,介導細胞免疫應答;以表達IL-4、IL-5、...
