基本介紹
- 中文名:置換矩陣
- 外文名:permutation matrix
- 條件:m×n 的矩陣如 m≤n且 PP′=E
- P′是:P的轉置矩陣
- E是:m階單位方陣
- 類別:數學術語
判定定理
嚴格定義




性質
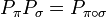


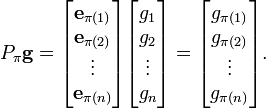

置換矩陣與置換
例子
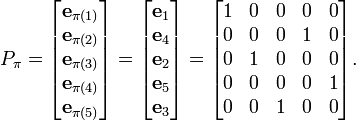





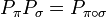


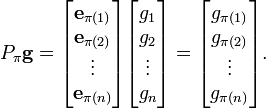

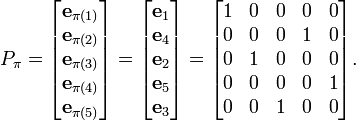

在數學上,特別是在矩陣理論中,置換矩陣是一個方形二進制矩陣,它在每行和每列中只有一個1,而在其他地方則為0。設P 是一個 m×n 的 (0,1) 矩陣,如果 m...
《矩陣分析與套用》是2004年9月1日清華大學出版社出版的一本圖書,作者是張賢達。本書將矩陣的分析分為梯度分析、奇異值分析、特徵分析、子空間分析與投影分析五大...
《矩陣論及其工程套用》是2015年清華大學出版社出版的圖書,作者是張賢達、周杰。...... 2.1.2置換矩陣與互換矩陣.302.1.3廣義置換矩陣與選擇矩陣322.1.4廣義...
《H-矩陣類的理論及套用》專門研究具有廣泛套用背景的H-矩陣類。全書共5章,第1章介紹有關的預備知識;第2章至第4章詳細闡述正定矩陣類、穩定矩陣類、對角占優...
所謂置換矩陣,是指交換一個n*n的單位矩陣的兩行得到的矩陣(線上性代數中,這種操作叫做矩陣的初等變換)。置換矩陣的每行/列都只有一個1,其餘元素全為0。 det相...
行的初等置換矩陣為 ,高斯變換矩陣為 。記 , 則可以證明:P 是排列矩陣,並且PA=LU。因此,矩陣 A 的部分主元消元過程實現了 A 的一個部分主元三角分解。主...
線上性代數中, LU分解(LU Decomposition)是矩陣分解的一種,可以將一個矩陣分解為一個單位下三角矩陣和一個上三角矩陣的乘積(有時是它們和一個置換矩陣的乘積)。...
數學上,克羅內克積是兩個任意大小的矩陣間的運算。克羅內克積是張量積的特殊形式,以德國數學家利奧波德·克羅內克命名。...
可以證明,所有的矩陣A都可以分解成一個上三角矩陣U、一個下三角矩陣L以及一個置換矩陣P的乘積: 。這時,矩陣A的行列式可以寫成:·分塊矩陣的行列式並不能簡單地...
矩陣變換有如下形式:A=P*L*U,P矩陣為置換矩陣,L時下三角形式,U是上三角形式 [2] 。參數介紹: M(input)INTEGER矩陣A的行數,M>=0。N (input)INTEGER矩陣...
