基本介紹
- 中文名:方陣函式
- 外文名:det
- 功能:求一個方陣的行列式
- 類型:計算機函式
函式簡介
語法格式
返回方陣X的行列式值。如果X僅包含一個整數元素,返回的結果d也是一個整數。
[L,U]=lu(A)
語句A=[1 2 3;45 6;7 8 9]得到
相關函式
程式示例
性質
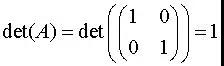 性質1
性質1
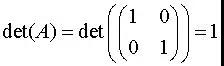 性質1
性質1det是一個計算機函式,在FreeMat、Matlab中,該函式用於求一個方陣(square matrix)的行列式(Determinant)。...
☆ 15世紀中期進入英語,直接源自古典拉丁語的detectus(detegere的過去分詞):de (不,分) + tegere (住蓋),意為揭開蓋住之物。...
Billoudet Davy,法國籍足球運動員。...... Billoudet Davy .Euro Sport[引用日期2014-06-26] 詞條標籤: 人物 V百科往期回顧 詞條統計 瀏覽次數:次 編輯次數:1...
《Videodet》是一款Android平台的套用。...... Videodet致力於提供一個無與倫比的娛樂體驗,而我們這樣做通過參與和賦權我們的內容提供商和客群的每一步。分享生活,...
Det. Tom Blake,主要作品《Wadd: The Life and Times of John C. Holmes》。...... Det. Tom Blake,主要作品《Wadd: The Life and Times of John C. Hol...
ADGJDET.exe是Creative創新音效卡的一部分。...... ADGJDET.exe是Creative創新音效卡的一部分。中文名 adgjdet 進程名稱: ADGJdet 出品者: Creative Technology Ltd...
進程檔案: adgjdet 或者 adgjdet.exe...... 進程檔案: adgjdet 或者 adgjdet.exe進程名稱: ADGJdet描述:ADGJDET.exe是Creative創新音效卡的一部分。...
接地電阻測試儀—DET4TD除了使用簡單外,還能自動檢測P級和C級的狀態,並把他顯示在顯示屏上。...
Galden DET是全氟聚醚產品,化學性質極其穩定。...... Galden DET化學結構中具有柔軟的乙醚結合體,即使高沸點等級也具有低粘度、低流動點的特點。...
Chanudet Coralie,法國籍足球運動員。...... Chanudet Coralie .Euro Sport[引用日期2014-06-03] 詞條標籤: 人物 V百科往期回顧 詞條統計 瀏覽次數:次 編輯次數...
Shinko Erdet,阿爾巴尼亞籍足球運動員。...... Shinko Erdet .Euro Sport[引用日期2014-09-13] 詞條標籤: 人物 V百科往期回顧 詞條統計 瀏覽次數:次 編輯次數:...
Robin Detje,演員,主要作品《魚雷》。...... 2008 魚雷 Helene Hegemann Jule Böwe,Robin Detje 演員 [1] 參考資料 1. Robin Detje ..[引用日期2014-01-...
矩陣行列式是指矩陣的全部元素構成的行列式,設A=(aij)是數域P上的一個n階矩陣,則所有A=(aij)中的元素組成的行列式稱為矩陣A的行列式,記為|A|或det(A)。若...
行列式在數學中,是一個函式,其定義域為det的矩陣A,取值為一個標量,寫作det(A)或 | A | 。無論是線上性代數、多項式理論,還是在微積分學中(比如說換元積分...
底特律(Detroit),位於經緯度42°19′N,83°2′W,建立於1815年,面積約370.2Km2,其中陸地面積為359.4Km2,水域面積為11Km2。海拔最高點位於城市西北部,海拔約為...
DNV認證全稱DNV-DET NORSKE VERITAS,是一個權威,專業,獨立的非營利性基金組織,挪威船級社成立於1864年,總部位於挪威首都奧斯陸。...
挪威船級社(DET NORSKE VERITAS)成立於1864年,總部位於挪威首都奧斯陸,是一家全球領先的專業風險管理服務機構,以“捍衛生命與財產安全,保護環境”為宗旨的獨立基金...
數據分析師 是數據師Datician['detɪʃən]的一種,指的是不同行業中,專門從事行業數據蒐集、整理、分析,並依據數據做出行業研究、評估和預測的專業人員。...
3 SD_DET 輸入 外擴存儲卡的數據輸入 4 SD_CLK 輸出 外擴存儲卡的時鐘信號 5 SD_DI 輸入 外擴存儲卡的數據輸入 6 SD_CS 輸出 外擴存儲卡的片選信...
4.A的全部順序主子式det( )>0。(A能夠作Cholesky分解的充要條件)cholesky分解證明方式 編輯 設A= >0,則A的所有順序主子式為正>0, i=1,2,...,n...
