基本介紹
定義介紹


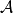

群的情形
模的情形
例子



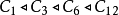



相關定理



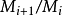
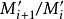

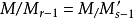



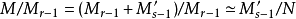
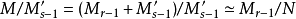
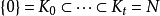






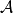




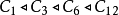






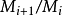
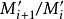

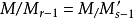



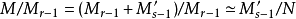
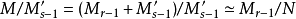
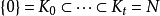



合成列(composition series)一種特殊類型的子群列。在抽象代數中,合成列是借著將代數對象(如群、模等等)拆解為簡單的成分,以萃取不變數的方式之一。...
合併單元格,指的是在辦公軟體中,excel將兩個或多個位於同一行或者同一列的單元格合併成一個單元格。合併單元格的操作多用於Word中的表格或Excel及表格控制項中.大...
合成金屬(synthetic metals) 一類不含金屬元素單質但具有金屬導電性的化合物。目前研究較多的有聚乙炔、鈣鈦礦型氧化物、鎢青銅等。聚乙炔柔曲性好,可撓性好,可用...
合成營,是指有多個兵種所組成的營級作戰單位,中國的合成營中包含有坦克、步兵、炮兵、工兵分隊,幾乎囊括了陸軍的所有基礎兵種,在營一級上就解決了步坦協同、步...
通過RNA提取、反轉錄等流程做出來cDNA片段是比較傳統經典的方式。但缺點是流程較長,且耗時耗力。 現在國外比較流行的是直接合成基因。其實原理是通過先合成長DNA單...
雙烯合成即狄爾斯-阿爾德反應(Diels-Alder反應,或譯作狄爾斯-阿德爾,第爾斯-阿德爾等等),由共軛雙烯與烯烴或炔烴反應生成六元環的反應,是有機化學合成反應中...
合成材料又稱人造材料,是人為地把不同物質經化學方法或聚合作用加工而成的材料,其特質與原料不同,如塑膠、合金(部分合金)等。 塑膠、合成纖維和合成橡膠號稱20...
特別是第二次世界大戰以後,合成部隊發展到一個新的階段。不少國家陸軍中出現了飛彈部隊、電子對抗部隊,還有的把直升機部隊(分隊)列為陸軍師以上的建制單位,營、...
高壓合成指在高壓(經常還有高溫)下合成常態時不能生成或難於生成的物質的過程。...... 高壓合成指在高壓(經常還有高溫)下合成常態時不能生成或難於生成的物質的過...
相干合成的技術方案按是否通過外界手段來干預探測並校正相位誤差可分為主動式的閉環有源相位控制和被動式的自組織鎖相運行雷射器陣列兩大類。...
合成類固醇又被稱為雄性合成類固醇激素,同化類固醇,促蛋白合成類固醇,包括皋酮及其衍生物。它與存在於機體性器官、肝、心、大腦、肌肉等部位的雄性激素受 體( AR ...
系統合成system synthesi。又稱系統綜合。是指如柯按一定的目標套用各種數學方法進行化工系統的最優組合。...
有機化學合成反應中非常重要的碳碳鍵形成的手段之一,也是現代有機合成里常用的反應之一。...
合成佯謬,經濟學術語,是指把局部合理的經濟學判斷,簡單地匯加起來,可能導致全局錯誤的結論。...
雙官能度的小分子單體,通過縮聚反應生成線形聚合物,同時伴隨著小分子副產物生成的聚合過程稱之線形縮聚反應,簡稱為線性合成。...
已合成有無色、黃色、綠色及藍色品種,大多數為黃色。晶體可由八面體、立方體、...過去只有GE公司擁有此類技術,且處理方式被列為最高機密。然而隨著世界技術水平的...
對於有限群,若爾當-赫爾德定理表明,這個分解過程可以得到該群的唯一的合成列(最多相差一個置換)。在2008年完成的有限單群分類工作是數學史上一個重要的里程碑。...
對於有限群 [1] ,有一個等價的定義為:一可解群為一有著其商群皆為質數目的循環群之合成列的群。此一定義會等價是因為每一個簡單阿貝爾群都是有質數目的循環...
第一個化學合成前列腺素E1類抗潰瘍藥,有強大的抑制胃酸分泌作用和防止潰瘍形成作用,能抑制的胃酸包括基礎胃酸分泌和由於組胺五肽胃泌素、食物或咖啡刺激引起的胃酸分泌...
必需脂肪酸是指機體生命活動必不可少,但機體自身又不能合成,必須由食物供給的多不飽和脂肪酸(PUFA)。必需脂肪酸主要包括兩種,一種是ω-3系列的α-亞麻酸(18:3...
將已有序的子序列合併,得到完全有序的序列;即先使每個子序列有序,再使子序列段間有序。若將兩個有序表合併成一個有序表,稱為二路歸併。...
本書介紹了基於無人水下航行器舷側陣的多目標探測技術,主要分為基於合成孔徑技術的多目標探測技術和基於多輸入多輸出陣列處理技術的多目標探測技術兩大部分。全書共...
蛋白質序列資料庫列資料庫 編輯 序列資料庫是生物信息資料庫中最基本的資料庫,...包括免疫球蛋白、T細胞受體、少於8個胺基酸殘基的小肽、合成序列、專利序列等。...
地塞米松(Dexamethasone,簡稱DXMS)於1957年首次合成,並列名於世界衛生組織基本藥物標準清單之中,為基礎公衛體系必備藥物之一。地塞米松價格低廉,在美國一個月療程通常...
