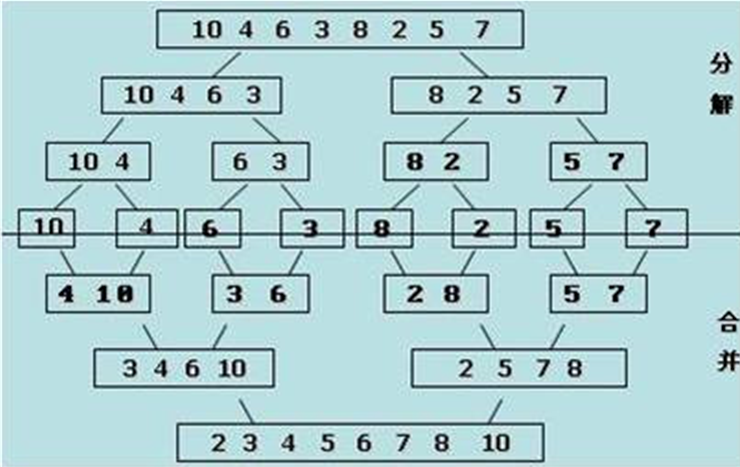
歸併排序（MERGE-SORT）是建立在歸併操作上的一種有效的排序算法,該算法是採用分治法（Divide and Conquer）的一個非常典型的套用。將已有序的子序列合併，得到完全有序的序列；即先使每個子序列有序，再使子序列段間有序。若將兩個有序表合併成一個有序表，稱為二路歸併。
基本介紹
- 中文名：歸併排序
- 外文名：Merge sort
- 穩定性：穩定
- 時間複雜度：O(n log n)
- 空間複雜度：T（n)
- 發明者：約翰·馮·諾伊曼
歸併操作,算法描述,比較,用途,排序,求逆序對數,示例代碼,複雜度,歸併算法,套用實例,
歸併操作
歸併操作(merge)，也叫歸併算法，指的是將兩個順序序列合併成一個順序序列的方法。
如 設有數列{6，202，100，301，38，8，1}
初始狀態：6,202,100,301,38,8,1
第一次歸併後：{6,202},{100,301},{8,38},{1}，比較次數：3；
第二次歸併後：{6,100,202,301}，{1,8,38}，比較次數：4；
第三次歸併後：{1,6,8,38,100,202,301},比較次數：4；
總的比較次數為：3+4+4=11；
逆序數為14；
算法描述
歸併操作的工作原理如下：
第一步：申請空間，使其大小為兩個已經排序序列之和，該空間用來存放合併後的序列
第二步：設定兩個指針，最初位置分別為兩個已經排序序列的起始位置
第三步：比較兩個指針所指向的元素，選擇相對小的元素放入到合併空間，並移動指針到下一位置
重複步驟3直到某一指針超出序列尾
將另一序列剩下的所有元素直接複製到合併序列尾
比較
歸併排序是穩定的排序.即相等的元素的順序不會改變.如輸入記錄 1(1) 3(2) 2(3) 2(4) 5(5) (括弧中是記錄的關鍵字)時輸出的 1(1) 2(3) 2(4) 3(2) 5(5) 中的2 和 2 是按輸入的順序.這對要排序數據包含多個信息而要按其中的某一個信息排序,要求其它信息儘量按輸入的順序排列時很重要。歸併排序的比較次數小於快速排序的比較次數，移動次數一般多於快速排序的移動次數。
用途
排序
求逆序對數
具體思路是，在歸併的過程中計算每個小區間的逆序對數，進而計算出大區間的逆序對數（也可以用樹狀數組來求解）
scala代碼：
objectMainextendsApp{ varreverse_pairs = 0//逆序數 defmsort[T](cmp:(T, T) => Boolean)(l:List[T]):List[T] = { defmerge(l1:List[T], l2:List[T]):List[T]=(l1, l2)match{ case(Nil, _) => l2 case(_, Nil) => l1 case(x::left1, y::left2) => if(cmp(x, y)) x::merge(left1, l2) else{ reverse_pairs += l1.length y::merge(l1, left2) } } valn = l.length / 2 if(n == 0) return l else{ val(l1, l2) = l.splitAt(n) merge(msort(cmp)(l1), msort(cmp)(l2)) } } println(msort((x:Int, y:Int) => x<y)(List(5, 4, 3, 2, 7,6 ))) println(reverse_pairs)}#include<cstdio>const int MAXN=200005;int n, a[MAXN], temp[MAXN];long long ans;void count(int l, int r){ if(r == l) return ;//結束條件 int m = (l + r) >> 1; count(l, m); count(m + 1, r);//二分查找 int i = l, j = m + 1, k = l; while(j <= r || i <= m) { if(j > r || (i <= m && a[i] < a[j])) temp[k++] = a[i++]; else temp[k++] = a[j++], ans += m - i + 1; } for(i = l; i <= r; i++) a[i] = temp[i];}int main(){ scanf("%d", &n); for(int i = 1; i <= n; i++) scanf("%d", &a[i]); count(1, n);//調用函式 printf("%lld", ans);//輸出 return 0;}示例代碼
歸併排序原理
歸併排序具體工作原理如下（假設序列共有n個元素）：
將序列每相鄰兩個數字進行歸併操作（merge)，形成floor(n/2+n%2)個序列，排序後每個序列包含兩個元素
將上述序列再次歸併，形成floor(n/4)個序列，每個序列包含四個元素
重複步驟2，直到所有元素排序完畢
示例代碼
Swift語言
//歸併排序func mergeSort(_ arr: inout [Int]) { var gap = 1; while gap < arr.count { mergePass(&arr, gap: gap); gap *= 2; }}//分解合併序列，gap表示子序列的元素個數func mergePass(_ arr: inout [Int], gap: Int) { var i = 0; let count = arr.count; while i + 2 * gap - 1 < count { mergeArray(&arr, low: i, mid: i + gap - 1, high: i + 2 * gap - 1); i += 2 * gap; } //合併剩餘的序列 if i + gap - 1 < count { mergeArray(&arr, low: i, mid: i + gap - 1, high: count - 1); }}//合併兩個序列func mergeArray(_ arr: inout [Int], low: Int, mid: Int, high: Int) { var i = low; var j = mid + 1; var k = 0; var array = Array<Int>(repeating: 0, count: high - low + 1); while i <= mid && j <= high { if arr[i] < arr[j] { array[k] = arr[i]; i += 1; k += 1; } else { array[k] = arr[j]; j += 1; k += 1; } } while i <= mid { array[k] = arr[i]; i += 1; k += 1; } while j <= high { array[k] = arr[j]; j += 1; k += 1; } //將排序好的序列複製回原數組 k = 0; for i in low...high { arr[i] = array[k]; k += 1; }}var array = [2, 5, 8, 9, 10, 4, 3, 16, 1, 7, 8];mergeSort(&array);print(array);Go語言
func mergeSort(r []int) []int { length := len(r) if length <= 1 { return r } num := length / 2 left := mergeSort(r[:num]) right := mergeSort(r[num:]) return merge(left, right)}func merge(left, right []int) (result []int) { l, r := 0, 0 for l < len(left) && r < len(right) { if left[l] < right[r] { result = append(result, left[l]) l++ } else { result = append(result, right[r]) r++ } } result = append(result, left[l:]...) result = append(result, right[r:]...) return}Java語言
package algorithm;public class MergeSort { // private static long sum = 0; /** * * <pre> * * 二路歸併 * * 原理：將兩個有序表合併和一個有序表 * * </pre> * * * * @param a * * @param s * * 第一個有序表的起始下標 * * @param m * * 第二個有序表的起始下標 * * @param t * * 第二個有序表的結束下標 * * */ private static void merge(int[] a, int s, int m, int t) { int[] tmp = new int[t - s + 1]; int i = s, j = m, k = 0; while (i < m && j <= t) { if (a[i] <= a[j]) { tmp[k] = a[i]; k++; i++; } else { tmp[k] = a[j]; j++; k++; } } while (i < m) { tmp[k] = a[i]; i++; k++; } while (j <= t) { tmp[k] = a[j]; j++; k++; } System.arraycopy(tmp, 0, a, s, tmp.length); } /** * * * * @param a * * @param s * * @param len * * 每次歸併的有序集合的長度 */ public static void mergeSort(int[] a, int s, int len) { int size = a.length; int mid = size / (len << 1); int c = size & ((len << 1) - 1); // -------歸併到只剩一個有序集合的時候結束算法-------// if (mid == 0) return; // ------進行一趟歸併排序-------// for (int i = 0; i < mid; ++i) { s = i * 2 * len; merge(a, s, s + len, (len << 1) + s - 1); } // -------將剩下的數和倒數一個有序集合歸併-------// if (c != 0) merge(a, size - c - 2 * len, size - c, size - 1); // -------遞歸執行下一趟歸併排序------// mergeSort(a, 0, 2 * len); } public static void main(String[] args) { int[] a = new int[]{4, 3, 6, 1, 2, 5}; mergeSort(a, 0, 1); for (int i = 0; i < a.length; ++i) { System.out.print(a[i] + " "); } }}C#語言
public static void Sort(int[] a, int f, int e){ if (f < e) { int mid = (f + e) / 2; Sort(a, f, mid); Sort(a, mid + 1, e); MergeMethid(a, f, mid, e); }}private static void MergeMethid(int[] a, int f, int mid, int e){ int[] t = new int[e - f + 1]; int m = f, n = mid + 1, k = 0; while(n <= e && m <= mid) { if (a[m] > a[n]) t[k++] = a[n++]; else t[k++] = a[m++]; } while (n < e + 1) t[k++] = a[n++]; while (m < mid + 1) t[k++] = a[m++]; for (k = 0, m = f; m < e + 1; k++, m++) a[m] = t[k];}Python語言
def MergeSort(lists): if len(lists) <= 1: return lists num = int( len(lists) / 2 ) left = MergeSort(lists[:num]) right = MergeSort(lists[num:]) return Merge(left, right)def Merge(left,right): r, l=0, 0 result=[] while l<len(left) and r<len(right): if left[l] <= right[r]: result.append(left[l]) l += 1 else: result.append(right[r]) r += 1 result += list(left[l:]) result += list(right[r:]) return resultprint MergeSort([1, 2, 3, 4, 5, 6, 7, 90, 21, 23, 45])
C語言
#include <stdlib.h>#include <stdio.h>void Merge(int sourceArr[],int tempArr[], int startIndex, int midIndex, int endIndex){ int i = startIndex, j=midIndex+1, k = startIndex; while(i!=midIndex+1 && j!=endIndex+1) { if(sourceArr[i] > sourceArr[j]) tempArr[k++] = sourceArr[j++]; else tempArr[k++] = sourceArr[i++]; } while(i != midIndex+1) tempArr[k++] = sourceArr[i++]; while(j != endIndex+1) tempArr[k++] = sourceArr[j++]; for(i=startIndex; i<=endIndex; i++) sourceArr[i] = tempArr[i];}//內部使用遞歸void MergeSort(int sourceArr[], int tempArr[], int startIndex, int endIndex){ int midIndex; if(startIndex < endIndex) { midIndex = startIndex + (endIndex-startIndex) / 2;//避免溢出int MergeSort(sourceArr, tempArr, startIndex, midIndex); MergeSort(sourceArr, tempArr, midIndex+1, endIndex); Merge(sourceArr, tempArr, startIndex, midIndex, endIndex); }}int main(int argc, char * argv[]){ int a[8] = {50, 10, 20, 30, 70, 40, 80, 60}; int i, b[8]; MergeSort(a, b, 0, 7); for(i=0; i<8; i++) printf("%d ", a[i]); printf("\n"); return 0;}PHP語言
//merge函式將指定的兩個有序數組(arr1,arr2)合併並且排序//我們可以找到第三個數組,然後依次從兩個數組的開始取數據哪個數據小就先取哪個的,然後刪除掉剛剛取過///的數據function al_merge($arrA,$arrB){ $arrC = array(); while(count($arrA) && count($arrB)){ //這裡不斷的判斷哪個值小,就將小的值給到arrC,但是到最後肯定要剩下幾個值, //不是剩下arrA裡面的就是剩下arrB裡面的而且這幾個有序的值,肯定比arrC裡面所有的值都大所以使用 $arrC[] = $arrA['0'] < $arrB['0'] ? array_shift($arrA) : array_shift($arrB); } return array_merge($arrC, $arrA, $arrB);}//歸併排序主程式function al_merge_sort($arr){ $len = count($arr); if($len <= 1) return $arr;//遞歸結束條件,到達這步的時候,數組就只剩下一個元素了,也就是分離了數組 $mid = intval($len/2);//取數組中間 $left_arr = array_slice($arr, 0, $mid);//拆分數組0-mid這部分給左邊left_arr $right_arr = array_slice($arr, $mid);//拆分數組mid-末尾這部分給右邊right_arr $left_arr = al_merge_sort($left_arr);//左邊拆分完後開始遞歸合併往上走 $right_arr = al_merge_sort($right_arr);//右邊拆分完畢開始遞歸往上走 $arr = al_merge($left_arr, $right_arr);//合併兩個數組,繼續遞歸 return $arr;}$arr = array(12, 5, 4, 7, 8, 3, 4, 2, 6, 4, 9);print_r(al_merge_sort($arr));Pascal語言
program mergesort_1;const maxn=7;type arr=array[1..maxn] of integer;var a,b,c:arr; i:integer;procedure merge(r:arr; l,m,n:integer; var r2:arr); var i,j,k,p:integer; begin i:=l; j:=m+1; k:=l-1; while (i<=m) and (j<=n) do begin k:=k+1; if r[i]<=r[j] then begin r2[k]:=r[i]; i:=i+1 end else begin r2[k]:=r[j]; j:=j+1; end end; if i<=m then for p:=i to m do begin k:=k+1; r2[k]:=r[p]; end; if j<=n then for p:=j to n do begin k:=k+1; r2[k]:=r[p]; end; end;procedure mergesort(var r,r1:arr; s,t:integer); var k:integer; c:arr; begin if s=t then r1[s]:=r[s] else begin k:=(s+t)div2; mergesort(r,c,s,k); mergesort(r,c,k+1,t); merge(c,s,k,t,r1) end; end;begin write('Enterdata:'); for i:=1 to maxn do read(a[i]); mergesort(a,b,1,maxn); for i:=1 to maxn do write(b[i]:9); writeln;end.//============================================program mergesort_2;const max=100000;var a,r:array[1..max] of longint; n,i:longint;procedure msort(s,t:longint); var m,i,j,k:longint; begin if s=t then exit; m:=(s+t) div 2; msort(s,m); msort(m+1,t); i:=s; j:=m+1; k:=s; while (i<=m) and (j<=t) do begin if a[i]<a[j] then begin r[k]:=a[i]; inc(i); inc(k); end else begin r[k]:=a[j]; inc(j); inc(k); end; end; while i<=m do begin r[k]:=a[i]; inc(i); inc(k); end; while j<=t do begin r[k]:=a[j]; inc(j); inc(k); end; for i:=s to t do a[i]:=r[i]; end;begin readln(n); for i:=1 to n do read(a[i]); msort(1,n); for i:=1 to n do writeln(a[i]);end.Basic語言
Sub MergeSort(Array() As Integer, First As Integer, Last As Integer)Dim mid As Integer = 0If first<last Then mid = (first+last)\ 2MergeSort(Array, first, mid);MergeSort(Array, mid+1, last);Merge(Array, first, mid, last);End IfEnd Sub/*以下示例代碼實現了歸併操作。array[]是元素序列，其中從索引p開始到q位置，按照升序排列，同時，從(q+1)到r也已經按照升序排列，merge()函式將把這兩個已經排序好的子序列合併成一個排序序列。結果放到array中。*//*** 0 <= p <= q < r, subarray array[p..q] and array[q+1..r] are already sorted.* the merge() function merges the two sub-arrays into one sorted array.*/void Merge(int array[], int p, int q, int r){ int i,k; int begin1,end1,begin2,end2; int* temp = (int*)malloc((r-p+1)*sizeof(int)); begin1 = p; end1 = q; begin2 = q+1; end2 = r; k = 0; while((begin1 <= end1)&&( begin2 <= end2)) { if(array[begin1] <= array[begin2]){ temp[k] = array[begin1]; begin1++; } else { temp[k] = array[begin2]; begin2++; } k++; } while(begin1<=end1 || begin2<=end2) { if(begin1<=end1) { temp[k++] = array[begin1++]; } if(begin2<=end2) { temp[k++] = array[begin2++]; } } for (i = 0; i < =(r - p); i++) array[p+i] = temp[i]; free(temp);}JavaScript語言
使用遞歸的代碼如下。優點是描述算法過程思路清晰，缺點是使用遞歸，mergeSort()函式頻繁地自我調用。長度為n的數組最終會調用mergeSort()函式 2n-1次，這意味著一個長度超過1500的數組會在Firefox上發生棧溢出錯誤。可以考慮使用疊代來實現同樣的功能。
function merge(left, right){ var result=[]; while(left.length>0 && right.length>0){ if(left[0]<right[0]){ /*shift()方法用於把數組的第一個元素從其中刪除，並返回第一個元素的值。*/ result.push(left.shift()); }else{ result.push(right.shift()); } } return result.concat(left).concat(right);}function mergeSort(items){ if(items.length == 1){ return items;}var middle = Math.floor(items.length/2), left = items.slice(0, middle), right = items.slice(middle); return merge(mergeSort(left), mergeSort(right));}非遞歸算法（C++）
#include<iostream>#include<ctime>#include<cstring>#include<cstdlib>using namespace std;/**將a開頭的長為length的數組和b開頭長為right的數組合併n為數組長度，用於最後一組*/void Merge(int* data,int a,int b,int length,int n){ int right; if(b+length-1 >= n-1) right = n-b; else right = length; int* temp = new int[length+right]; int i=0, j=0; while(i<=length-1 && j<=right-1){ if(data[a+i] <= data[b+j]){ temp[i+j] = data[a+i];i++; } else{ temp[i+j] = data[b+j]; j++; } } if(j == right){//a中還有元素，且全都比b中的大,a[i]還未使用 memcpy(temp + i + j, data + a + i, (length - i) * sizeof(int)); } else if(i == length){ memcpy(temp + i + j, data + b + j, (right - j)*sizeof(int)); } memcpy(data+a, temp, (right + length) * sizeof(int)); delete [] temp;}void MergeSort(int* data, int n){ int step = 1; while(step < n){ for(int i=0; i<=n-step-1; i+=2*step) Merge(data, i, i+step, step, n); //將i和i+step這兩個有序序列進行合併 //序列長度為step //當i以後的長度小於或者等於step時，退出 step*=2;//在按某一步長歸併序列之後，步長加倍 }}int main(){ int n; cin>>n; int* data = new int[n]; if(!data) exit(1); int k = n; while(k--){ cin>>data[n-k-1]; } clock_t s = clock(); MergeSort(data, n); clock_t e = clock(); k=n; while(k--){ cout<<data[n-k-1]<<' '; } cout<<endl; cout<<"the algorithm used"<<e-s<<"miliseconds."<<endl; delete data; return 0;}遞歸算法：#include<iostream>using namespace std;void merge(int *data, int start, int mid, int end, int *result){ int i, j, k; i = start; j = mid + 1; //避免重複比較data[mid] k = 0; while (i <= mid && j <= end) //數組data[start,mid]與數組(mid,end]均沒有全部歸入數組result中去 { if (data[i] <= data[j]) //如果data[i]小於等於data[j] result[k++] = data[i++]; //則將data[i]的值賦給result[k]，之後i,k各加一，表示後移一位 else result[k++] = data[j++]; //否則，將data[j]的值賦給result[k]，j,k各加一 } while (i <= mid) //表示數組data(mid,end]已經全部歸入result數組中去了，而數組data[start,mid]還有剩餘 result[k++] = data[i++]; //將數組data[start,mid]剩下的值，逐一歸入數組result while (j <= end) //表示數組data[start,mid]已經全部歸入到result數組中去了，而數組(mid,high]還有剩餘 result[k++] = data[j++]; //將數組a[mid,high]剩下的值，逐一歸入數組result for (i = 0; i < k; i++) //將歸併後的數組的值逐一賦給數組data[start,end] data[start + i] = result[i]; //注意，應從data[start+i]開始賦值}void merge_sort(int *data, int start, int end, int *result){ if (start < end) { int mid = start + (end-start) / 2;//避免溢出int merge_sort(data, start, mid, result); //對左邊進行排序 merge_sort(data, mid + 1, end, result); //對右邊進行排序 merge(data, start, mid, end, result); //把排序好的數據合併 }}void amalgamation(int *data1, int *data2, int *result){ for (int i = 0; i < 10; i++) result[i] = data1[i]; for (int i = 0; i < 10; i++) result[i + 10] = data2[i];}int main(){ int data1[10] = { 1,7,6,4,9,14,19,100,55,10 }; int data2[10] = { 2,6,8,99,45,63,102,556,10,41 }; int *result = new int[20]; int *result1 = new int[20]; amalgamation(data1, data2, result); for (int i = 0; i < 20; ++i) cout << result[i] << " "; cout << endl; merge_sort(result, 0, 19, result1); for (int i = 0; i < 20; ++i) cout << result[i] << " "; delete[]result; delete[]result1; return 0;}二路歸併
ConstFI='in.txt';FO='out.txt';MaxN=10000;TypeTIndex=Longint;TDat=Array[0..MaxN]OfTIndex;VarN:TIndex;Dat:TDat;Tmp:TDat;ProcedureMerge(L,Mid,R:TIndex);VarP1,P2:TIndex;E1,E2:TIndex;P:TIndex;I:TIndex;BeginP1:=L;P2:=Mid+1;P:=L;RepeatIf(Dat[P1]<=Dat[P2])ThenBeginTmp[P]:=Dat[P1];Inc(P1);Inc(P);EndElseBeginTmp[P]:=Dat[P2];Inc(P2);Inc(P);End;Until(P1=Mid+1)Or(P2=R+1);If(P1=Mid+1)ThenBeginE1:=P2;E2:=R;EndElseBeginE1:=P1;E2:=Mid;End;ForI:=E1ToE2DoBeginTmp[P]:=Dat[I];Inc(P);End;End;ProcedureSort(L,R:TIndex);VarMid:TIndex=0;BeginMid:=(L+R)Shr1;If(L<Mid)ThenSort(L,Mid);If(Mid+1<R)ThenSort(Mid+1,R);Merge(L,Mid,R);ForMid:=LToRDoDat[Mid]:=Tmp[Mid];End;ProcedureInit;VarI:TIndex;BeginFillChar(Dat,SizeOf(Dat),0);Readln(N);ForI:=1ToNDoRead(Dat[I]);End;ProcedureMain;BeginSort(1,N);End;ProcedureFinal;VarI:TIndex;BeginForI:=1ToNDoWrite(Dat[I],'');Writeln;End;BeginAssign(Input,FI);Assign(Output,FO);Reset(Input);Rewrite(Output);Init;Main;Final;Close(Input);Close(Output);End.
Delphi
歸併排序完整原始碼例子：
//合併子函式procedureTForm1.MergePass(vardatas:arrayofInteger;left,mid,right:Integer);vartmpArr:arrayofInteger;arrLen:Integer;i,k:Integer;begin1,begin2,end1,end2:Integer;beginarrLen:=right-left+1;SetLength(tmpArr,arrLen);begin1:=left;end1:=mid;begin2:=mid+1;end2:=right;k:=0;while((begin1<=end1)and(begin2<=end2))dobeginif(datas[begin1]<datas[begin2])thenbegintmpArr[k]:=datas[begin1];Inc(begin1);endelsebegintmpArr[k]:=datas[begin2];Inc(begin2);end;inc(k);end;while(begin1<=end1)dobegintmpArr[k]:=datas[begin1];Inc(begin1);Inc(k);end;while(begin2<=end2)dobegintmpArr[k]:=datas[begin2];Inc(begin2);Inc(k);end;fori:=0to(right-left)dobegindatas[left+i]:=tmpArr[i];end;end;//排序主函式，left是數組左下標，0開始。right是數組右下標。procedureTForm1.MergeSort(vardatas:arrayofInteger;left,right:Integer);varmid:Integer;i:Integer;beginmid:=0;if(left<right)thenbeginmid:=(right+left)div2;showLog('中間索引：'+inttostr(mid));MergeSort(datas,left,mid);MergeSort(datas,mid+1,right);MergePass(datas,left,mid,right);showLog('--->'+getArrayString(datas));//顯示數組中間狀態end;end;//調用方法：procedureTForm1.btn1Click(Sender:TObject);varinArr:array[0..9]ofInteger;beginCopyMemory(@inArr[0],@CTabls[0],SizeOf(Integer)*10);showLog('輸入數據：'+getArrayString(inArr));MergeSort(inArr,0,High(inArr));showLog('輸出數據：'+getArrayString(inArr));end;複雜度
歸併排序比較占用記憶體，但卻是一種效率高且穩定的算法。
改進歸併排序在歸併時先判斷前段序列的最大值與後段序列最小值的關係再確定是否進行複製比較。如果前段序列的最大值小於等於後段序列最小值，則說明序列可以直接形成一段有序序列不需要再歸併，反之則需要。所以在序列本身有序的情況下時間複雜度可以降至O(n)
TimSort可以說是歸併排序的終極最佳化版本，主要思想就是檢測序列中的天然有序子段（若檢測到嚴格降序子段則翻轉序列為升序子段）。在最好情況下無論升序還是降序都可以使時間複雜度降至為O(n)，具有很強的自適應性。
最好時間複雜度 | 最壞時間複雜度 | 平均時間複雜度 | 空間複雜度 | 穩定性 | |
傳統歸併排序 | O(nlogn) | O(nlogn) | O(nlogn) | T(n) | 穩定 |
改進歸併排序 | O(n) | O(nlogn) | O(nlogn) | T(n) | 穩定 |
TimSort | O(n) | O(nlogn) | O(nlogn) | T(n) | 穩定 |
註：文獻是一種改進的原地歸併算法，空間複雜度為O(1)。在表格里的改進歸併排序只是引入其預先判斷的這一步，這樣便可使傳統歸併排序時間複雜度降至O(n)。
歸併算法
定義
所謂歸併排序是指將兩個或兩個以上有序的數列（或有序表），合併成一個仍然有序的數列（或有序表）。這樣的排序方法經常用於多個有序的數據檔案歸併成一個有序的數據檔案。歸併排序的算法比較簡單。
基本思想方法：
（1）假設已經有兩個有序數列，分別存放在兩個數組s，r中；並設i，j分別為指向數組的第一個單元的下標；s有n個元素，r有m個元素。
（2）再另設一個數組a，k指向該數組的第一個單元下標。
（3）算法分析（過程）：
proceduremerge(s,r,a,i,j,k);begini1:=i;j1:=j;k1:=k;while(i1<n)and(j1<m)doifs[i1]<=r[j1]thenbegina[k]:=s[i1];i1:=i1+1;k:=k+1;endelsebegina[k]:=r[j1];j1:=j1+1;k:=k+1;end;whilei1<=ndobegina[k]:=s[i1];i1:=i1+1;k:=k+1;end;whilej1<=mdobegina[k]:=r[j1];j1:=j1+1;k:=k+1;end;end;
完整的C++原始碼
#include<iostream.h>voidMerge(intr[],intr1[],ints,intm,intt){inti=s;intj=m+1;intk=s;while(i<=m&&j<=t){if(r[i]<=r[j])r1[k++]=r[i++];elser1[k++]=r[j++];}if(i<=m)while(i<=m)r1[k++]=r[i++];elsewhile(j<=t)r1[k++]=r[j++];for(intn=s;n<=t;n++)r[n]=r1[n];}voidMergeSort(intr[],intr1[],ints,intt){if(s<t){intm=(s+t)/2;MergeSort(r,r1,s,m);MergeSort(r,r1,m+1,t);Merge(r,r1,s,m,t);}}voidmain(){intr[8]={10,3,5,1,9,34,54,565},r1[8];MergeSort(r,r1,0,7);for(intq=0;q<8;q++)cout<<""<<r[q];return0；}歸併排序的實現方法：
1.自底向上算法
#include<stdio.h>#include<time.h>voidMerge(int*a,intlow,intmid,inthigh){inti=low,j=mid+1,k=0;int*temp=(int*)malloc((high-low+1)*sizeof(int));while(i<=mid&&j<=high)a[i]<=a[j]?(temp[k++]=a[i++]):(temp[k++]=a[j++]);while(i<=mid)temp[k++]=a[i++];while(j<=high)temp[k++]=a[j++];memcpy(a+low,temp,(high-low+1)*sizeof(int));free(temp);}voidMergeSort(int*a,intn){intlength;for(length=1;length<n;length*=2){inti;for(i=0;i+2*length-1<=n-1;i+=2*length)Merge(a,i,i+length-1,i+2*length-1);if(i+length<=n-1)//尚有兩個子檔案，其中後一個長度小於length Merge(a,i,i+length-1,n-1);}}intmain(){intn;cin>>n;int*data=newint[n];if(!data)exit(1);intk=n;while(k--){cin>>data[n-k-1];}clock_ts=clock();MergeSort(data,n);clock_te=clock();k=n;while(k--){cout<<data[n-k-1]<<'';}cout<<endl;cout<<"thealgrothemused"<<e-s<<"miliseconds."<<endl;deletedata;return0;}2.自頂向下
voidMerge(intr[],intr1[],ints,intm,intt){inti=s;intj=m+1;intk=s;while(i<=m&&j<=t){if(r[i]<=r[j])r1[k++]=r[i++];elser1[k++]=r[j++];}while(i<=m)r1[k++]=r[i++];while(j<=t)r1[k++]=r[j++];for(intl=0;l<8;l++)r[l]=r1[l];}voidMergeSort(intr[],intr1[],ints,intt){if(s==t);else{intm=(s+t)/2;MergeSort(r,r1,s,m);MergeSort(r,r1,m+1,t);Merge(r,r1,s,m,t);}}套用實例
NOIP2013 提高組火柴排隊
#include<bits/stdc++.h>using namespace std;int c[1000005],t[1000005],mod=99999997;long long cnt=0;struct edge{ int num,i;}a[1000005],b[1000005];void merge(int l,int r){ if(l==r) return; int mid=(l+r)/2; merge(l,mid); merge(mid+1,r); int x=l,y=mid+1,tot=l; while(x<=mid&&y<=r) if(c[x]<=c[y]) t[tot++]=c[x++]; else { cnt+=(mid-x+1)%mod; cnt%=mod; t[tot++]=c[y++]; } while(x<=mid) t[tot++]=c[x++]; while(y<=r) t[tot++]=c[y++]; for(int i=l;i<= r;++i) c[i]=t[i];}bool cmp(edge a,edge b){ return a.num<b.num;}int main(){ int n; cin>>n; for(int i=1;i<=n;++i) { cin>>a[i].num; a[i].i=i; } for(int i=1;i<=n;++i) { cin>>b[i].num; b[i].i=i; } sort(a+1,a+n+1,cmp); sort(b+1,b+n+1,cmp); for(int i=1;i<=n;++i) c[a[i].i]=b[i].i; merge(1,n); cout<<cnt<<endl; return 0;}