計數排序是一個非基於比較的排序算法,該算法於1954年由 Harold H. Seward 提出。它的優勢在於在對一定範圍內的整數排序時,它的複雜度為Ο(n+k)(其中k是整數的範圍),快於任何比較排序算法。 當然這是一種犧牲空間換取時間的做法,而且當O(k)>O(n*log(n))的時候其效率反而不如基於比較的排序(基於比較的排序的時間複雜度在理論上的下限是O(n*log(n)), 如歸併排序,堆排序)
基本介紹
- 中文名:計數排序
- 外文名:Counting sort
- 提出人: Harold H. Seward
- 提出時間:1954
- 定義:非基於比較的排序算法
算法思想
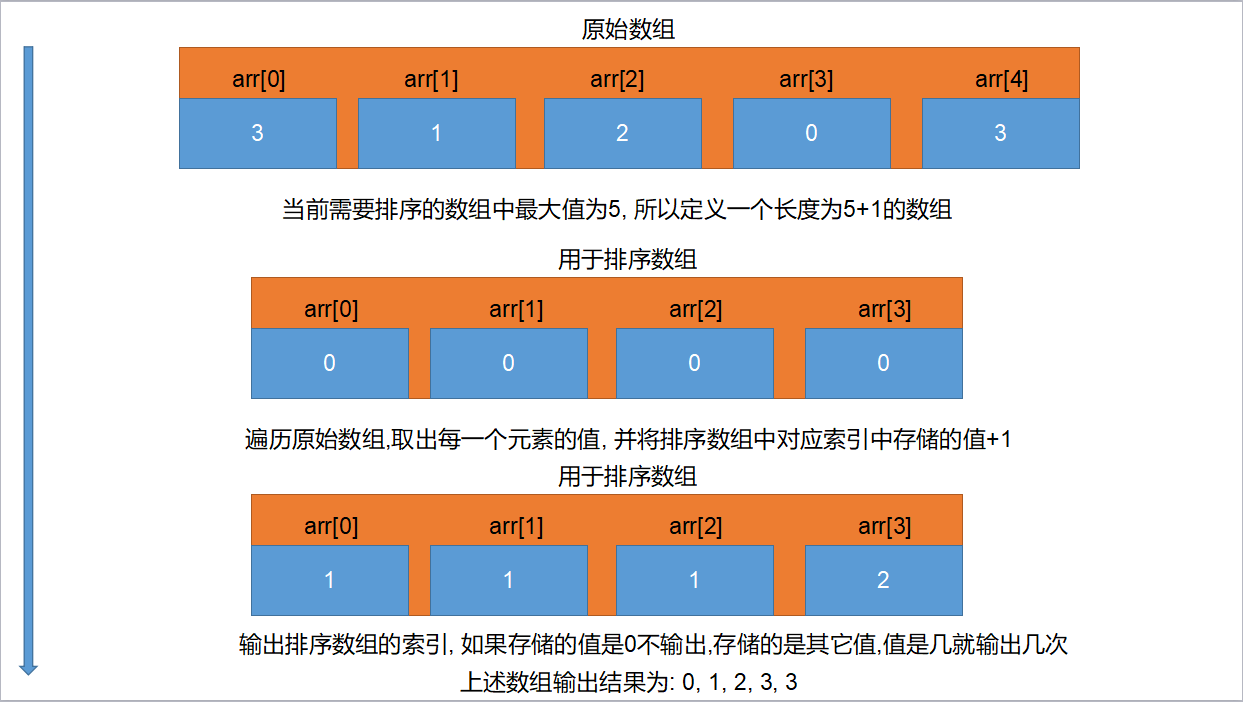
算法過程
算法描述
實現方法1:program counting_sort1;const max=100;var a,b,c:Array[1..max] of longint; i,j,k,n:longint;begin readln(n); for i:=1 to n do read(a[i]); fillchar(c,sizeof(c),0); for j:=1 to n do inc(c[a[j]]); for i:=2 to x{x是大於a[i]中任意值的任意數且x≤max}do c[i]:=c[i]+c[i-1]; for j:=n downto 1 do begin b[c[a[j]]]:=a[j]; dec(c[a[j]]); end; for i:=1 to n do writeln(b[i],' ');end.實現方法2:program counting_sort2;const max=100;var a:array[1..max] of longint; i,j,k,n,m,x:longint;begin readln(n); fillchar(a,sizeof(a),0);//初始清空 m:=0; for i:=1 to n do begin read(x); inc(a[x]); if x>m then m:=x;//找到最大的數 end; for i:=1 to m do if a[i]>0 then for j:=1 to a[i] do write(i,' ');end.#include <iostream>using namespace std;const int MAXN = 100000;const int k = 1000; // rangeint a[MAXN], c[MAXN], ranked[MAXN];int main() { int n; cin >> n; for (int i = 0; i < n; ++i) { cin >> a[i]; ++c[a[i]]; } for (int i = 1; i < k; ++i) c[i] += c[i-1]; for (int i = n-1; i >= 0; --i) ranked[--c[a[i]]] = a[i];//如果是i表達的是原數標號,a[i]就是排序後的正確序列 for (int i = 0; i < n; ++i) cout << ranked[i] << endl; return 0;}#include<stdio.h>#include<stdlib.h>#define MAXNUM 10void main(){ void CountSort(int data[],int n); int i,data[MAXNUM]; for(i=0;i<MAXNUM;i++) scanf("%d",&data[i]); CountSort(data,MAXNUM); for(i=0;i<MAXNUM;i++) printf("%d ",data[i]); printf("\n");}void CountSort(int data[],int n){ int i,j,count,*data_p; data_p=(int*)malloc(sizeof(int)*n); for(i=0;i<n;i++)//初始化data_p data_p[i]=0; for(i=0;i<n;i++) { count=0; for(j=0;j<n;j++)//掃描待排序數組 if(data[j]<data[i])//統計比data[i]值小的值的個數 count++; if(data_p[count]!=0)//對於相等非0的數據,應向後措一位。數據為0時,因數組data_p被初始化為0,故不受影響。 count++; data_p[count]=data[i];//存放到data_p中的對應位置 } //用於檢查當有多個數相同時的情況 i=0,j=n; while(i<j) { if(data_p[i]==0) { temp=i-1; data_p[i]=data_p[temp]; }//of if i++; }//of while for(i=0;i<n;i++)//把排序完的數據複製到data中 data[i]=data_p[i]; free(data_p);//釋放data_p}//針對c數組的大小,最佳化過的計數排序publicclassCountSort{ publicstaticvoidmain(String[]args){ //排序的數組 int a[]={100,93,97,92,96,99,92,89,93,97,90,94,92,95}; int b[]=countSort(a); for(inti:b){ System.out.print(i+""); } System.out.println(); } public static int[] countSort(int[]a){ int b[] = new int[a.length]; int max = a[0],min = a[0]; for(int i:a){ if(i>max){ max=i; } if(i<min){ min=i; } }//這裡k的大小是要排序的數組中,元素大小的極值差+1 int k=max-min+1; int c[]=new int[k]; for(int i=0;i<a.length;++i){ c[a[i]-min]+=1;//最佳化過的地方,減小了數組c的大小 } for(int i=1;i<c.length;++i){ c[i]=c[i]+c[i-1]; } for(int i=a.length-1;i>=0;--i){ b[--c[a[i]-min]]=a[i];//按存取的方式取出c的元素 } return b; }}public int[] CountSort(int[] a){ int[] b = new int[a.Length]; int max = a[0]; int min = a[0]; foreach (int item in a) { if(item > max) { max = item; } else if (item < min) { min = item; } } int k = max - min + 1; int[] c = new int[k]; for (int i = 0; i < a.Length; i++) { c[a[i] - min] += 1; } for (int i = 1; i < c.Length; i++) { c[i] = c[i] + c[i - 1]; } for (int i = a.Length-1; i >= 0; i--) { b[--c[a[i] - min]] = a[i]; } return b;}def sort(a): n=len(a) b=[None]*n for i in range(n): p=0 q=0 for j in range(n): if a[j]<a[i]: p+=1 elif a[j]==a[i]: q+=1 for k in range(p,p+q): b[k]=a[i] print b
func countSort(arr []int) { maxVal := 0 length := len(arr) for i := 0; i < length; i ++ { if arr[i] > maxVal { maxVal = arr[i] } } tmp := make([]int, maxVal+1) for i := 0; i < length; i ++ { tmp[arr[i]] += 1 } j := 0 for i := 0; i < maxVal+1; i ++ { for tmp[i] > 0 { arr[j] = i j ++ tmp[i] -- } }}