基本介紹
- 中文名:非齊次線性方程組
- 外文名:Nonhomogeneous linear equations
- 含義:常數項不全為零的線性方程組
- 充要條件:充要條件是rank(A)=n。
定義
解法
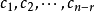

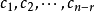
常數項不全為零的線性方程組。...... 非齊次線性方程組定義 編輯 常數項不全為零的線性方程組稱為非齊次線性方程組。非齊次線性方程組的表達式為:Ax=b...
線性方程組是各個方程關於未知量均為一次的方程組(例如2元1次方程組)。對線性方程組的研究,中國比歐洲至少早1500年,記載在公元初《九章算術》方程章中。線性方程...
齊次線性方程組:常數項全部為零的線性方程組。如果m<n(行數小於列數,即未知數的數量大於所給方程組數),則齊次線性方程組有非零解,否則為全零解。...
定理2 設非齊次線性方程組Ax=b的係數矩陣A= ,若rankA=n,則(1) 矩陣ATA是對稱正定矩陣;(2) n階線性方程組ATAx=ATb有唯一的解。...
1.5.1 非齊次線性方程組 251.5.2 齊次線性方程組 28本章小結 29習題一 31自測題一 34第二章 矩陣及其運算 372.1 矩陣的概念 37...
線性方程組的解的一般形式,又稱為一般解。...... 2.對於線性方程組(定理)設 是 元非齊次線性方程組 的一個特解, 為其導出組 的基礎解系,則 為 的通解或...
本書包含矩陣、行列式、線性方程組、向量、特徵值與特徵向量、二次型等內容.各章的每一節後都配有習題,書末附有習題參考答案.本書還給出了一些比較簡單的線性...
評註: 若未知向量的坐標而要判斷能否線性表出的問題,通常是轉換為非齊次線性方程組是否有解的討論,如果向量的坐標沒有給出而問能否線性表出,通常用線性相關及秩...
《線性代數2》是普通高等學校工科本科各專業基礎課線性代數教材,內容包括:線性空間、線性變換與矩陣、行列式及其套用、線性方程組、特徵值和特徵向量、二次型.《線性...
1.7.1 非齊次線性方程組(22)1.7.2 齊次線性方程組(24)習題1(24)第2章 矩陣及其運算(28)2.1 矩陣(28)2.1.1 矩陣的定義(28)...
《線性代數初步》根據教育部最新制定的《高職高專教育線性代數課程教學基本要求》編寫的。《線性代數初步》共分四章,分別為行列式、矩陣、n維向量和線性方程組。書中...
4.3.2向量組的秩與矩陣的秩的關係習題4.3第四節 線性方程組的解的結構4.4.1齊次線性方程組4.4.2非齊次線性方程組習題4.4第5章 線性空間與歐氏空間...
3.4.2向量組的秩853.4.3矩陣與向量組秩的關係853.5線性方程組解的結構873.5.1齊次線性方程組解的結構873.5.2非齊次線性方程組解的結構93...
第一節線性方程組解的判定定理20第二節齊次線性方程組20第三節非齊次線性方程組22第五章矩陣的特徵值與特徵向量24第一節矩陣的特徵值與特徵向量24...
1.5.1 非齊次線性方程組 1.5.2 齊次線性方程組 本章小結 習題 自測題 第二章 矩陣及其運算 2.1 矩陣的概念 2.1.1 矩陣的定義 2.1.2 幾種特...
概念將非齊次線性方程組右端的常數項換為零,得到的齊次線性方程組,稱為該非齊次線性方程組的導出齊次線性方程組或相應的齊次線性方程組,簡稱為導出組。即為齊次...
非齊次線性方程組AX=b 有唯一解;A的行(列)向量組線性無關;任一n維向量可由A的行(列)向量組線性表示。其實以上條件全部是等價的。詞條標籤: 文化術語 , 字詞...
克萊姆法則,又譯克拉默法則(Cramer's Rule)是線性代數中一個關於求解線性方程組的定理。它適用於變數和方程數目相等的線性方程組,是瑞士數學家克萊姆(1704-1752)...
他還給出展開行列式的“拉普拉斯定理”,發展了解非齊次微分線性方程組的常數變數法,研究了複變函數的積分和有限差分,並對物理學中的毛細管作用、熱學理論、粒子論、...
