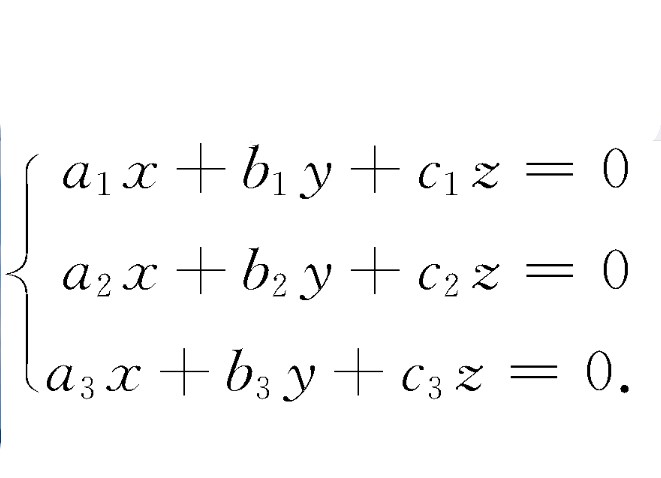三元齊次線性方程組(system of ternary homogeneous linear equations)亦稱三元一次齊次方程組,是一種特殊的線性方程組,即方程組中的各個方程的常數項都是零的三元線性方程組。在初等數學中,三元齊次線性方程組常指aix+biy+ciz=0(i=1,2,3)組成的方程組。三元齊次線性方程組總有零解(x,y,z)=(0,0,0),當係數行列式不等於零時,它只有零解,當係數行列式等於零時,有無窮多個非零解。
基本介紹
- 中文名:三元齊次線性方程組
- 外文名:system of ternary homogeneous linear equations
- 別稱:三元一次齊次方程組
- 所屬學科:數學
- 所屬問題:初等代數(方程)
基本介紹



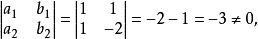
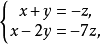


齊次線性方程組