普呂克坐標

普呂克坐標(Pliicker coordinates)是指格拉斯曼空間中可合元素的坐標。

普呂克是德國數學家、物理學家。生於德國埃爾伯費爾德(Elberfeld) ，卒于波恩。攻讀于波恩、海德堡(Heidelberg)、柏林、巴黎等大學。1824年在馬爾堡(Marburg)大學獲得博士學位，1825年赴波恩大學任教，1828年升為特別教授，1833年任柏林大學特別教授。

基本介紹

• 中文名：普呂克坐標
• 外文名：Pliicker coordinates
• 領域：數學
• 空間：格拉斯曼空間
• 對象：可合元素
• 重要人物：格拉斯曼、普呂克

概念

普呂克坐標是格拉斯曼空間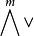 中可合元素的坐標。若{e₁，e₂，…，e_n}是V的基，則 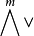的可合元素v₁∧v₂∧…∧v_m可表示為：

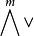
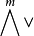
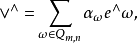
可合元素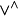 的坐標{a_ω|ω∈Q_m，n}稱為子空間〈v₁，v₂，…，v_m〉的普呂克坐標。存在著許多判別 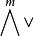的元素為可合元素的充分必要條件，通常就是判別坐標{a_ω|ω∈Q_m，n}為普呂克坐標的充分必要條件。例如，若

為 的任一元素，則z為可合元素的充分必要條件是存在m×n的矩陣A=(a_ij)使得：

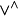
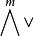
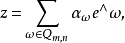
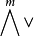
a_ω=det A[1，2，…，m|ω] (ω∈Q_m，n)，其中A[1，2，…，m|ω]表示A的ω(1)，ω(2)，…，ω(m)列子方陣。

格拉斯曼空間

格拉斯曼空間亦稱反對稱張量空間。是一個最常見的張量對稱類，即當G=S_m，χ=ε(符號特徵標)時的張量對稱類。通常寫為：

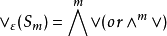
可合元素則寫為：

T(S_m，ε)v^∧=v^∧=v₁∧v₂∧…∧v_m，

又稱為v₁，v₂，…，v_m的外積。反對稱張量空間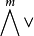 具有許多很好的性質。例如，v₁∧v₂∧…∧v_m≠0的充分必要條件是v₁，v₂，…，v_m線性無關；又如：

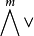
v₁∧v₂∧…∧v_m=au₁∧…∧u_m≠0的充分必要條件是〈v₁，v₂，…，v_m〉=〈u₁，u₂，…，u_m〉且維數是m。也有：

其中n=dim V。若{e₁，e₂，…，e_m}是V的基，則{e^∧_ω|ω∈Q_m，n}是 的基。例如 的基為{e₁∧e₂，…，e₁∧e_n…，e_i∧e_j，…，e_n-1∧e_n}(其中i<j)。

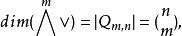
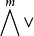
可合元素

可合元素亦稱可合張量。一類特殊的張量。張量空間：

的元素稱為張量，其中屬於Im 的元素(即張映射 的值)稱為可合張量，又稱為可分解張量或可分解元素，記為 (v₁，v₂，…，v_m)=v₁ v₂ … v_m=v。可合張量v₁v₂…v_m也稱為v₁，v₂，…，v_m的張量積。可合張量有下面的重要性質：

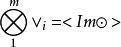
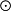
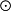
1.若v₁ v₂ … v_m=u₁ u₂ … u_m，則對任意ψ∈M(V₁，V₂，…，V_m;W)有ψ(v₁，v₂，…，v_m)=ψ(u₁，u₂，…，u_m).

2.v₁ v₂ … v_m=0的充要條件是有某一個v_i=0.

3.v₁ v₂ … v_m=u₁ u₂ … u_m≠0的充分必要條件是存在c_i∈K使v_i=c_iu_i≠0 (i=1，2，…，m)且

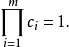
基

代數數域作為有理數域上的線性空間的基。設K=Q(θ)為n次代數數域，記θ=θ⁽¹⁾，並以θ⁽²⁾，…，θ⁽ⁿ⁾表示θ所適合的不可約多項式的其他n-1個根。於是，K中任一數α必可表為α=α(θ)=a₁+a₁θ+…+a_n-1θ^n-1，其中a_j為有理數。設α=α⁽¹⁾，則稱α^(k)=α(θ^(k))(k=2，3，…，n)為α的共軛數，稱S(α)=α⁽¹⁾+α⁽²⁾+…+α⁽ⁿ⁾=α(θ⁽¹⁾)+α(θ⁽²⁾)+…+α(θ⁽ⁿ⁾)與N(α)=α⁽¹⁾，α⁽²⁾，…，α⁽ⁿ⁾=α(θ⁽¹⁾)，α(θ⁽²⁾)，…，α(θ⁽ⁿ⁾)為α的跡與范.有S(α+β)=S(α)+S(β)，N(αβ)=N(α)N(β)。S(α)，N(α)均為有理數。特別地，若α為有理數時，則S(α)=nα，N(α)=α.若α為代數整數，則S(α)，N(α)均為代數整數，從而為有理整數。若在K中能找到一組數α₁，α₂，…，α_n，使K中任何一數都可以惟一地表為a₁α₁+a₂α₂+…+a_mα_m的形式，其中a_j(1≤j≤m)為有理數，則稱α₁，α₂，…，α_m為K之基。K中任何基所含元素個數相同，且均等於n。若α₁，α₂，…，α_n及β₁，β₂，…，β_n為R(θ)之兩組基，則有有理數a_jk(1≤j，k≤n)使

α_i=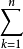 a_jkβ_k　(1≤j≤n)且其係數行列式|a_jk|≠0。

人物簡介

格拉斯曼

德國數學家。生於斯德丁(Stettin，現為波蘭什切青Szczecin)，卒於同地。1831年在柏林學習神學，後來自學物理、數學和拉丁語，還熟練掌握了印度梵文。1836年繼承父業，後回鄉任中學物理和數學教師，業餘進行科學研究，發表一系列有創見的論著，並寫了若干中學教科書。格拉斯曼的代表作是《線性擴張理論》(Die lineale Ausdehnungslehre，1844)。首次提出關於多維歐氏空間理論的系統學說，引入矢量的一般運算。此外，他與哈密頓同時分別建立起超複數理論，通過討論開創了張量分析研究。格拉斯曼的另一著作是《算術教本》(Lehrbuchder Arithmetik，1861)。該書對中學算術的基礎作了科學論述，給出自然數加法與乘法的定義，證明了兩種運算的一些基本性質。還特別討論了無理數的基本理論。另外，他曾用自己的計算方法研究n階曲線，提出矩陣化為三角式的方法，並論述了該方法與射影變換分類間的關係等。格拉斯曼的其他貢獻涉及電學、聲學、植物學和語言學等領域，他編纂的梵文詞典(1875)至今仍在廣泛使用。

普呂克

德國數學家、物理學家。生於德國埃爾伯費爾德(Elberfeld) ，卒于波恩。攻讀于波恩、海德堡(Heidelberg)、柏林、巴黎等大學。1824年在馬爾堡(Marburg)大學獲得博士學位，1825年赴波恩大學任教，1828年升為特別教授，1833年任柏林大學特別教授。1834年受聘為哈雷(Halle)大學教授。1836年以後任波恩大學教授。1867年當選為法國科學院院士。1868年獲得英國科普利獎章。普呂克在幾何學方面有重大的貢獻。他的第一部重要著作《解析幾何的發展》(Analytischg-eometrische Entwicklungen，1828，1831)分為兩卷出版，其中討論了直線、圓和二次曲線的平面解析幾何學，運用縮寫的符號和幾何的推導，以優美的方式證明了該領域中的許多結論和定理。在該書中的第二卷中，解析地闡述了對偶性原理。他還引入了所謂三角形坐標，與同時期麥比烏斯引入的重心坐標相比，屬於另一種類型的齊次點坐標。普呂克獨立地把配極的概念推廣到所有的平面代數曲線，並研究了代數曲線的焦點、兩曲面的密切等問題。在1835年出版的《解析幾何系統》(System deranalytischen Geometrie，1835)一書中，討論了三次平面曲線，給出了三次曲線的構造及分類。在1839年發表的著作《代數曲線理論》(Theorie der algebraischenKurven)中，考察了無窮遠點鄰域內代數曲線的性質，不但考慮了漸近(直)線，也顧及到漸近二次曲線和與給定三次曲線密切的曲線，並證明了著名的“普呂克公式”。該公式揭示出曲線的秩和類數的關係。據此還推得進一步的結果：對於無奇點的三次曲線，不可能找出多於3個的實拐點。普呂克晚年同他的年青助手克萊因合作，發展了(代數)線幾何學理論，其中，他運用對偶方式引入了6個齊次線坐標Pij，現在稱為“普呂克坐標”，建立了線叢(complexes)、線匯(congruences)等新的概念，並將(直線)線叢和線匯(linear com-plexes and congruences)分類，為二次線叢的研究奠定了基礎。在物理學方面，普呂克也做了許多工作。他探討了稀薄氣體中的放電過程，觀測到三種氫光譜線;還發現了電氣石晶體的磁現象(1847)。

\