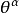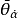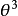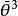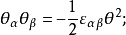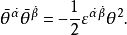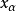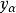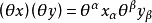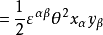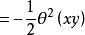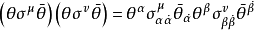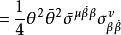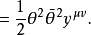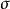Grassmann代數是格拉斯曼在研究線性空間理論時發展出來的代數結構,被費羅貝尼烏斯和達布成功地用於解決普發夫問題。後來E.嘉當系統地發展了外形式和外微分式理論,並且廣泛地用於幾何學的研究,外代數從此有了寬廣的套用領域。
基本介紹
- 中文名:grassmann數
- 外文名:Grassmann number
- 全稱:Grassmann代數
- 套用學科:量子力學術語
- 範疇:數理科學
- 涉及:外代數
概述,基本原理,
概述
數學家Grassmann在19世紀末葉引入了一個新的數系,這一數系的基本特性是它的反對易性。Grassmann代數是格拉斯曼在研究線性空間理論時發展出來的代數結構,被費羅貝尼烏斯和達布成功地用於解決普發夫問題。後來E.嘉當系統地發展了外形式和外微分式理論,並且廣泛地用於幾何學的研究,外代數從此有了寬廣的套用領域。
基本原理
Grassmann數滿足如下的對易關係:
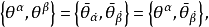
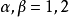
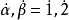
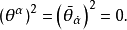
以後我們約定:Grassmann數與所有玻色類型的場量對易,與所有費米類型的場量反對易。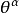 和
和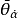 的標積定義為:
的標積定義為: