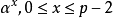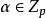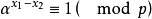有限幾何

有限幾何(finite geometry)是指含有限個點的幾何結構，在組合設計理論中，所涉及的幾何結構是指一類特別的關聯繫統，這種系統中有兩類不定義的元素，分別稱為點和線，以及點線之間的關聯關係，對這樣的關聯繫統加上不同類型的限制，即規定不同的公理，便得到各種類型的有限幾何結構。

基本介紹

• 中文名：有限幾何
• 外文名：finite geometry
• 所屬學科：數理科學
• 相關概念：有限域、仿射平面等

定義

一個有限射影幾何包含著由點P、q、…組成的有限集以及由的子集L、M、……組成的子集簇，這些子集稱為線，並且這些子集滿足公理(i)一(iv)(若，我們稱P在L上或L通過P)。

(i) 通過任意兩不同的點P和q存在唯一的一條線(用(Pq)表示)。

(ii) 每條線至少包含3點。

(iii) 若不同的線L，M有公共點P，且若q，r為L上不等於P的點，及s，t為M上不等於P的點，則線(qt)和(rs)也有一公共點(看圖1)。

(iv) 對任意點P至少存在兩條不含P的線，而對任意線L至少存在兩個不在L上的點。

射影幾何的子空間必是的子集S且S滿足：

(v) 若P，q是S的不同的點則S包含線(Pq)上所有的點。

圖1 公理（iii）

子空間的實例就是內的點和線以及自身。超平面H是最大的正規子空間，所以是唯一的完全包含H的子空間。

定義 從一射影幾何的子空間中去掉一固定的超平面H(叫做在無窮遠處的超平面)的點就得到一仿射或歐幾里德幾何。所形成的那些集都叫做仿射幾何的子空間。

在一射影幾何或仿射幾何中的一點集t，若對一切，則X不屬於包含T-{X}的最小子空間，T叫做獨立的。例如，任何不在一線上的三點啤做獨立的。如果 r 是在子空間S中獨立點的最大集的尺度，S的維數是r-1。特別地，若S=這就定義了射影幾何的維數。

射影幾何PG(m，q) 射影幾何和仿射幾何中最重要的是從有限域得到的那些情況。

設GF(q)為一有限域且假定m≥2．的點以非0的(m+1)重

表示，並且規定

和

代表相同的點，這裡為GF(q)的任意非0元。這些叫做點的齊次坐標。存在個非0的(m+1)重而每點出現q-1次，所以在中點的數目為()/(q一1)。

通過兩不同點和的線由點

構成，這裡均不為0。因為對於，存在q²—1種選擇而每點在上式中出現q-1次，一線包含q十1點。

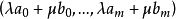
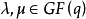
明顯地滿足公理(i)，(ii)。

仿射平面上的直線

作為有限域的一個套用，下面介紹有限幾何的概念。

定義1 設F是有限域，仿射平面AP(F)由下列兩個集合組成：

① 點集 ，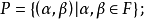

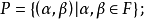
② 直線集 ={ 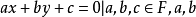不全為0}。

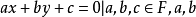
不難證明仿射平面AP(F)具有普通歐幾里得平面的性質：

① 過兩個不同的點只能作一條直線；

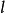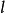② 過一直線 外的點P只能作一條直線 與 不相交。

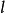
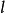
由於AP(F)是定義在有限域上，因而P與L都是有限集合，且有以下計數定理。

定理1 設F是有限域且 ，AP(F)是F上的仿射平面，則有

①

②

③ 每條直線恰通過n個點；

④ 每個點恰在n+1條直線上。

有限域理論在組合設計中有很好的套用。

離散橢圓曲線

有一種密碼系統是利用離散橢圓曲線進行編碼的，那么什麼是橢圓曲線呢?我們先從實平面上的橢圓曲線說起，設a，b為實數，實平面上的曲線方程的圖形是以x軸為對稱軸的曲線，稱為橢圓曲線(elliptic curve)．根據判別式的三種情況和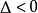，橢圓曲線有三種類型。例如，方程，曲線由兩部分組成，在左半平面是一個類似於橢圓的一條封閉曲線，而右半平面是一條不封閉的趨向無窮的曲線。

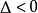
類似，我們可以在有限幾何中研究橢圓曲線，它的定義如下。

定義2 設p>3為素數，有限域，且，則滿足同餘式

的點的集合E稱為F上的離散橢圓曲線(discrete elliptic curve)．並假定E中有一個特殊點O。在E中定義加法如下：設，則

其中

定義。

上面式子中的運算均為mod p的運算。

可以證明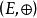是可換群．元素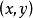的逆元為。

離散對數

各種形式的同餘方程在密碼學中有很多套用，對於指數是未知數的同餘方程，就是所謂離散對數(discrete logarithm)問題：

定義3 設p>3為素數，是一個本原元，，求整數滿足

x存在且惟一的，稱x為的以為底的離散對數，並記作。

首先我們看一下離散對數的存在惟一性．這是因為是一個本原元，它是的生成元，所以均有使．若有J，則由得，因而，在[0，p-2]範圍內是惟一確定的。

我們更關心的是如何計算離散對數．由於是在有限域上計算離散對數，自然會想到把所有的冪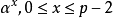都計算出來，從而找出所對應的x。