簡介
由有限次中心射影的積定義的兩條直線間的一一對應變換稱為一維射影變換。
 一維射影變換
一維射影變換由有限次中心射影的積定義的兩個平面之間的一一對應變換稱為二維射影變換。
 二維(高維)射影變換
二維(高維)射影變換因為正交變換、相似變換、仿射變換都保持共線三點的單比不變,必然保持共線四點的交比不變,所以這些變換都是射影變換。
交比
定義
若A、B、C、D為直線l上的任意四點,稱兩個單比和的比為這四點的
交比或複比,
定理
中心射影保持共線四點的交比不變。
線束的射影變換
定義
平面上兩個線束的射影變換及線束的交比。如下圖所示,平面上有兩個線束O,O’,若它們所有對應線的交點共線,則稱這兩個線束的對應為中心射影。類似點列的射影變換,有限次中心射影的積稱為線束間的射影變換。
定理1
射影變換保持線束的交比不變。射影坐標系定義如下,直線L上的一維射影坐標系由原點O,單位點E與無窮遠點I定義任意一點A的坐標由交比x=R(A,E,O,I)定義。由交比定義得,E,O,I點的坐標分別為
。
二維平面上的射影坐標系由不共線的四點定義,即O(原點),E(單位點),Ix(x軸上的無窮遠點)與Iy(y軸上的無窮遠點)定義,平面上任意一點A的射影坐標由兩個交比定義。
定理2
平面上全部射影變換的集合構成群
平面上全部射影變換的集合構成群
稱之為射影變換群,仿射變換群、相似變換群、正交變換群都是它的子群。
仿射變換
仿射變換是射影變換的特殊情況,當定義中心射影的線束為互相平行的直線時,變換稱為仿射變換,由於線束中的直線互相平行,顯然,仿射變換保持交比不變。
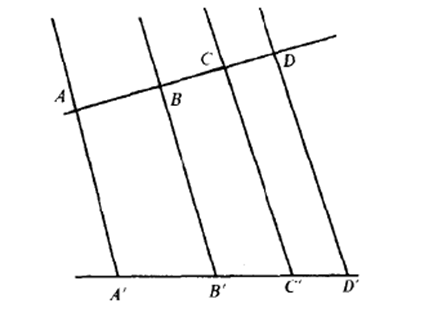 仿射變換
仿射變換相關知識
射影平面
對射影平面的理解是從局部到整體的擴展過程。先從無窮遠元素、
射影直線的理解入手,再到射影平面定義的理解,最後利用射影平面的模型來揭示射影平面的結構,想像它的形狀,幫助初學者更好地理解射影平面的結構與性質。在射影幾何的基本內容中,初學者對射影平面尤感興趣,但又覺得其極為抽象、難以理解,這主要是與我們的直觀認識不一致引起的。因此,從射影平面上的無窮遠點、無窮遠直線、射影直線的理解入手,在理解這些抽象概念的同時,即理解射影平面上元素的特點,接著理解射影平面的定義,最後給出射影平面的模型以幫助理解射影平面的形象。
理解射影平面上的元素
對射影平面的理解建立在對無窮遠元素以及射影直線的透徹理解的基礎上,射影平面上元素的特點決定了射影平面的性質。
理解無窮遠元素的約定:
在射影平面上有約定:在平面內對於任何一組平行線引入唯一一點叫無窮遠點,此點在組中每一直線上而不在此組外的任何直線上。一平面內一切無窮遠點的集合組成一條直線叫無窮遠直線。我們應對這約定有深刻的理解;這約定的途徑是給平行直線添加交點,而且不破壞點與直線的兩個基本關係,即兩條不同直線確定唯一交點,兩個不同的點確定唯一一條直線;對應於平面上的每一個方向,有唯一無窮遠點;每一條直線上有且僅有一個無窮遠點;平面上添加的無窮遠點的個數等於過原點的直線數,平面上任意兩條直線有且僅有一個交點;無窮遠直線上的點均為無窮遠點;平面上任何無窮遠點均在無窮遠直線上;每一條普通直線與無窮遠直線有且僅有一個交點為該直線上的無窮遠點;每一個平面上有且僅有一條無窮遠直線。
理解射影直線的定義:
射影直線是指射影平面上的直線。射影直線的定義是:在歐氏直線上添加一個無窮遠點後得到仿射直線,在仿射直線上,如果把普通點與無窮遠點同等看待而不加區分,那么這條直線就叫做射影直線。根據上述約定以及射影直線的定義,我們通過區別歐氏直線與射影直線來理解射影直線的形象,比如:歐氏直線是不封閉的,一點分直線為兩部分,三點排成唯一順序,如下左圖。射影直線是封閉的,一點不能分直線為兩部分,三點不能排成唯一順序,所以,可以選取圓作為射影直線的模型。
理解射影平面的定義:
射影平面的定義比較抽象,它在射影平面的理解中是必不可少的一個環節。射影平面的定義是:歐氏平面上添加一條無窮遠直線即可得仿射平面,在仿射平面上,如果對普通元素與無窮遠元素不加區分,即可得射影平面。結合射影直線的定義可得出對射影平面的如下理解:射影平面上的直線是封閉的,且任意兩條直線有一個交點,每一條直線上有唯一一個無窮遠點,射影平面上有唯一一條無窮遠直線。根據上述的理解,還可得出射影平面與歐氏平面的不同,如:在歐氏平面上一條直線可以把平面分為兩個區域,兩條相交直線可以把平面分為四個區域;而在射影平面上,一條直線並不能把該平面分為兩個區域,因為連線兩個點的線段有兩個,其中只有一個線段與另一直線相交,而另一線段一定不與此直線相交。兩直線只能把射影平面分為兩個區域,如下圖的兩部分和Ⅱ的兩部分都是相通的,而Ⅰ、Ⅱ兩部分是不相通的。因為在射影平面上,直線是封閉的,且兩直線有且僅有一個交點。
用射影平面的模型來理解射影平面的形象
在上述理解的基礎上,為了進一步理解射影平面的整體性質,給出射影平面以下的幾種模型。
模型一:
我們知道,默比烏斯帶的特點是具有單側性,即沿著這帶子上任一處出發塗一種顏色,則可以不越過邊界將它全部塗遍(即原紙帶的兩面都塗上同樣的顏色)。我們從下面這模型出發,藉助於默比烏斯帶的單側性來說明射影平面也是單側的。我們可以作一個默比烏斯帶,它是射影平面的一部份。如果把默比烏斯帶的兩個同樣的邊界都粘和起來,就可以得到射影平面。我們可以想像得出射影平面的單側性和封閉性。在歐氏空間裡,我們只能看到射影平面的一部分。
模型二:
射影平面的模型還可以如下方式給出,設在歐氏空間中給定一個原點O為球心的球面,當把球面上對徑點粘和為一點,視為射影點,並把對徑點粘和為一點的球面上的大圓視為射影直線,則得到的圖形即為射影平面的一個模型。
在這模型中,射影直線都是封閉的,並且任意兩條射影直線都相交於一點。而且,是為了使得中心射影成為一一對應,才給平行線添加交點,引進了無窮遠點。從而由歐氏直線得到仿射直線,由仿射直線得到射影直線,而由歐氏平面得到仿射平面,由仿射平面得到射影平面。在這裡,此射影平面的模型還可以與仿射平面建立一一對應關係。事實上,取定與給定球面相切於一點的仿射平面α,以球心O為射影中心建立此模型Ψ到仿射平面α的中心射影,在此中心射影下,對於Ψ上的Ao點,即球面上的一對對徑點A和B,從球心O作通過A和B兩點的直線交仿射平面於點C,則點Ao與C對應,而由位於過球心O,平行於α的歐氏平面上的球面大圓所決定的射影直線,則對應於仿射平面上的無窮遠直線。這樣,就可以建立α上的點與Ψ上的點之間的一一對應。
模型三:
射影平面還可以有其它的模型。取過空間一點O的全部直線和平面,稱為一個把。對於仿射平面α上任一點,對應於把上的一條直線OA,α上的任意一條直線l對應於把里的一個平面β。把的每一條直線稱為一個“點”,其中每一個平面稱為一條直線,則這個把也是射影平面的一個模型,可把這模型稱為直線把模型。在這個模型里,滿足兩直線交於一個點。對於上述所討論的模型,是從通常空間加以改造而得出的,這有助於我們理解射影平面的結構與性質。
綜上所述,在射影平面上,直線是封閉的,每一條直線上都有一個無窮遠點,兩條直線有且僅有一個交點,射影平面從局部上看與歐氏平面相同,而從整體看,它是一個具有單側性的封閉曲面。
 一維射影變換
一維射影變換 二維(高維)射影變換
二維(高維)射影變換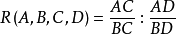

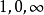
 仿射變換
仿射變換
