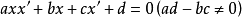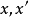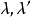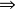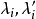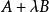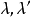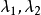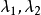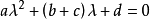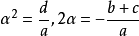一維射影變換(one-dimensional projective transformation)是指重疊一維基本形之間的射影對應。如果平面上兩個同類的一維基本形(同為點列或線束)是同底的或同心的，則稱為重疊的一維基本形，兩個重疊的一維基本形的射影對應，也就是一個一維基本形到自身的射影對應稱為一維射影變換。射影變換是射影對應的特殊情形，因此其代數表達式也是非奇異線性變換(參見“射影變換”)，射影對應還可用參數法表示，即兩個一維基本形(同為點列和線束)A+λB與A+λ′B成射影對應的充要條件是任何元素的參數λ與對應元素的參數λ′之間滿足雙線性方程aλλ′+bλ+cλ′+d=0，其中a，b，c，d為常數且ad-bc≠0。反之，若λ，λ′滿足雙線性方程，則A+λB與A+λ′B間的對應是射影對應。
基本介紹
- 中文名：一維射影變換
- 外文名：one-dimensional projective transformation
- 所屬學科：數學
- 所屬問題：高等幾何(射影幾何)
- 簡介：重疊一維基本形之間的射影對應
一維射影變換的定義,一維射影變換的參數表示,一維射影變換的分類,不變元素,一維射影變換分類,不變元素的性質,
一維射影變換的定義
對應是指兩個集合的元素之間的關係，而變換則是指同一個集合的元素之間的關係．
定義1 一個一維基本形到其自身的射影對應稱為一維射影變換。
此時可把一個一維基本形看作兩個重疊的一維基本形，即兩個同底的點列
或者兩個同束心的線束
。為了說清楚元素與其像元素，我們常常把同一個一維基本形看作兩個一維基本形，一個是變換前的，叫做第一基本形；一個是經射影變換作用之後的，叫做第二基本形，這樣，當我們研究一個一維基本形上的射影變換時，這個基本形中的每一個元素就都有著雙重身份，既是第一基本形的元素，又是第二基本形的元素。
顯然，射影變換是特殊的射影對應，所有關於射影對應討論的結果都適用於射影變換。
一維射影變換的參數表示
一維射影變換的代數表示式就是
定義2 形如
的方程稱為關於
的雙線性方程。
顯然，一維射影變換的非齊次坐標表達式為一個雙線性方程。
定理1 一維基本形上的一個變換為射影變換
其對應元素的參數
滿足一個雙線性方程
證明：因為點列和線束的非齊次參數表示具有完全相同的代數結構，所以在本定理的證明中無需特別指明所論一維基本形是點列還是線束。
“
”設兩個重疊的一維基本形
。取定基元素A，B，則對任意的
，有
。設此射影對應由
(i=1，2，3，
各不相同)決定，而
與
為任一對對應元素。據Steiner定義，有
“
”由(2)式成立，可直接驗證其滿足Steiner定義，即(2)所決定的變換是雙射，且保持任意四對對應元素的交比不變，證明從略。
我們把(2)稱為一維射影變換的參數表示。對於一維射影對應，利用參數表示常常會比用代數表示式(1)更有其方便之處。
雙線性方程(2)可以取作一維射影變換的定義，並且，從代數的角度說，這個定義可以不限於點列，對線束也成立。
在定理1的證明過程中，若捨棄重疊條件，結論仍然成立．故(2)也可以作為一般的一維射影對應的定義，即使是兩個不同類的一維基本形也同樣適用。
一維射影變換的分類
不變元素
所謂不變元素，是指在一個變換下保持不變的元素。對不變元素的研究，歷來是各種幾何學的重要內容。
定理2 在複數範圍內，任一個一維射影變換至少有一個不變元素，非恆同的一維射影變換具有不多於兩個的相異不變元素。
證明：在(2)中，令
，得到
一維射影變換分類
考察(3)，其有根情況為
(1) 兩個相異的實根
, 對應著射影變換(2) 有兩個相異的實不變元素；
(2) 兩個相等的實根λ1，射影變換有兩個重合的實不變元素， 或者說只有惟一不變元素；
(3) 兩個共軛虛根，射影變換有兩個共軛的虛不變元素。
定義3設
為一維射影變換，如果有兩個相異的實不變元素，則稱之為一個雙曲型射影變換；如果有兩個重合的實不變元素，則稱之為一個拋物型射影變換；如果有兩個共軛的虛不變元素，則稱之為一個橢圓型射影變換。
不變元素的性質
關於雙曲型、橢圓型射影變換和拋物型射影變換，分別有下列兩個結論成立．
定理3 若一個一維射影變換具有兩個相異的不變元素，則任一對相異的對應元素與兩個不變元素所成的交比為常數，稱為此射影變換的特徵不變數。
證明： 設X，Y為一維基本形射影變換的兩個相異的不變元素，P,P'為任一對對應元素(非不變元素)，只要證(PP'，XY)=常數。
設X，Y，P，P'的坐標依次為
，則這四點的參數分別為
，代入(2)式並計算可求出
，故
(PP'，XY)=
=常數.
所以一維射影變換(2)的特徵不變數為。
定理4設一維拋物型射影變換的不變元素參數為
，而
為任一對相異對應元素的參數，則
證明：欲證之式可以變形為
化簡即得（4）式。
